Упругая линия балки
Изогнутая под действием нагрузок ось балки представляет собой плавную кривую, которая называется упругой линией. Деформация балки при изгибе характеризуется п р о г и б о м у и углом поворота поперечного с е ч е н и я, который равен углу а наклона касательной к упругой линии по отношению к оси z балки. Уравнения прогибов и углов поворота сечений в общем виде записываются так:
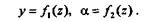
|
Из математики известно, что радиус кривизны кривой у = f1(z) в любой точке определяется по формуле
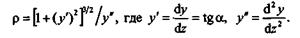
|
Ввиду малости деформаций (у)2 пренебрегаем (так как эта величина значительно меньше единицы), тогда
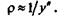
Ранеемы вывели формулу 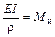 ; подставляя в нее приближенное
; подставляя в нее приближенное
значение радиуса кривизны, получим дифференциальное уравнение упругой линии балки:
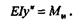
Чтобы получить уравнение  = f2(z), углов поворота сечений, надо это уравнение проинтегрировать один раз, причем ввиду малости деформаций будем считать, что
= f2(z), углов поворота сечений, надо это уравнение проинтегрировать один раз, причем ввиду малости деформаций будем считать, что
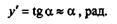
Для получения уравнения прогибов у = f1(z), надо дифференциальное уравнение проинтегрировать дважды.
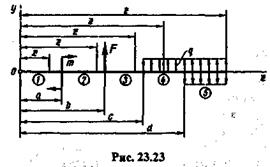
Рассмотрим балку постоянного сечения, нагруженную моментом те, сосредоточенной силой F и равномерно распределенной нагрузкой q,дающими положительные изгибающие моменты (рис. 23.23).
Начало координат возьмем на левом конце балки, ось у направим вверх, а ось z — вправо. Рассматриваемая балка имеет пять участков, каждому из которых соответствует свое уравнение моментов, уравнение прогибов и уравнение углов поворота сечений. Обратим внимание на то,
|
что упругая линия балки есть плавная кривая, следовательно, на границах участков значения углов поворота сечения и прогибов, вычисленных из уравнений соседних участков, будут совпадать. Интегрирование дифференциальных уравнений будем произ-
водить, не раскрывая скобок в уравнениях моментов, что сказывается лишь на значениях произвольных постоянных. 1-й участок:
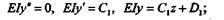
2-й участок:
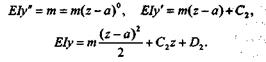
|
Подставив в уравнения первого и второго участков значение z = a,получим
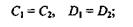
3-й участок:
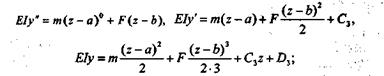
4-й участок:
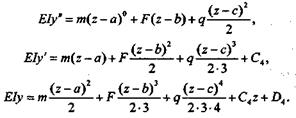
Так как на границах смежных участков справедливы уравнения и предыдущего и последующего участков, то
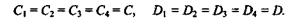
|
Обозначив  0угол поворота сечения в начале координат (в радианах), а у0— прогиб в начале координат, при z = 0 получим
0угол поворота сечения в начале координат (в радианах), а у0— прогиб в начале координат, при z = 0 получим
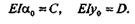
|
Так как каждой отдельной нагрузке в уравнениях соответствует отдельное слагаемое, в общем виде можно записать такие уравнения:
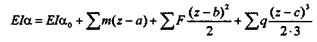
— обобщенное уравнение углов поворота сечений;
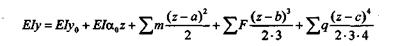
—обобщенное уравнение прогибов.
Если равномерно распределенная нагрузка заканчивается не в конце балки, то эту нагрузку следует мысленно продолжить до конца и добавить противоположно направленную нагрузку такой же интенсивности (рис. 23.23, участок 5). При этом в обобщенные уравнения углов поворота и прогибов добавится еще по одному слагаемому с отрицательным знаком, соответственно:
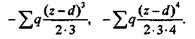
|
Знаки слагаемых в обобщенных уравнениях устанавливают по п р а -вилу знаков для изгибающих моментов.
Положительное значение у обозначает прогиб вверх, и наоборот; положительное значение а означает поворот сечения против часовой стрелки, и наоборот.
При пользовании обобщенными уравнениями следует помнить, что:
1) для балки, жестко защемленной левым концом,
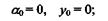
2) для балки, левый конец которой лежит на опоре,
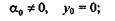
|
для определения а0 следует составить уравнение прогибов для второй опоры и приравнять его нулю;
3) в сечении с максимальным прогибом угол поворота сечения  = 0, так как в этой точке упругой линии касательная параллельна оси г.
= 0, так как в этой точке упругой линии касательная параллельна оси г.
Помимо расчетов на прочность балки нередко проверяют или рассчитывают на жесткость. Условие жесткости заключается в том, что максимальный прогиб (стрела прогиба f) или максимальный угол поворота не должны превышать допускаемых величин. Расчетные уравнения на жесткость имеют вид:
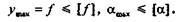
Допускаемую величину прогиба обычно задают в долях длины пролета l, например, для мостов [f]= 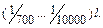 Допускаемый угол поворота сечения задают в долях радиана.
Допускаемый угол поворота сечения задают в долях радиана.
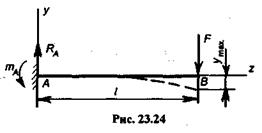
Пример 23.8. Определить прогиб уB свободного конца консольной балки АВ,изгибаемой сосредоточенной силой F (рис. 23.24.).
Решение. Реакция RA и момент защемления тА соответственно равны:
|
RA=F, mA=Fl.
Учитывая, что y0= 0, d0= 0, из обобщенного уравнения прогибов находим
EIyB=RAl3/6-mAl2/2.
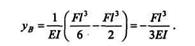
|
Подставив значения RA и тА,получим
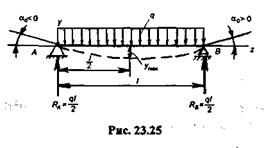
Пример 23.9. Определить максимальный прогиб и углы поворота сечений на опорах балки, показанной на рис.23.25.
Решение. В силу симметрии балки реакции опор равны
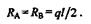
Поместим начало координат на левой опоре, тогда у0 = 0. Для определения Оо используем условие, что при z = l ув = 0.
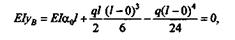
откуда  0 = -ql3/(24EI).Очевидно, что
0 = -ql3/(24EI).Очевидно, что  B = -
B = -  0.
0.
Наибольшие углы поворота имеют опорные сечения.
Максимальный прогиб находится посередине пролета балки, т. е. при z = l/2. Тогда:
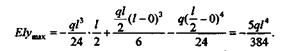
Следовательно,

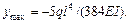
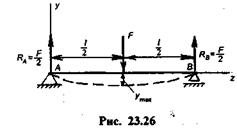
Пример 23.10. Определить максимальный прогиб и угол поворота на опорах балки, нагруженной посередине пролета сосредоточенной силой (рис.23.26).
|
Решение.Реакции равны F/2каждая и направлены снизу вверх.
Помещаем начало координат на левой опоре, тогда у0= 0.
Для определения 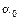 используем условие, что при z = l прогиб равен нулю (yB = 0):
используем условие, что при z = l прогиб равен нулю (yB = 0):
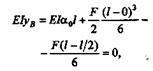
|
 откуда
откуда
Следовательно,
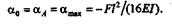
Ввиду симметрии угол поворота на правой опоре
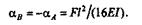
Максимальный прогиб будет при z = l/2,тогда
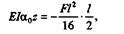
следовательно,
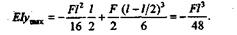
Окончательно
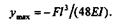
Балки равного сопротивления изгибу.При изгибе балок постоянного сечения (за исключением случая чистого изгиба) все сечения, кроме опасного, имеют излишний запас прочности, что свидетельствует о нерациональном использовании материала. Наиболее рациональной будет такая форма балки, при которой напряжения во всех поперечных сечениях будут равны допускаемому. Такие балки называются балками равного сопротивления изгибу.
Рассмотрим произвольное сечение балки равного сопротивления изгибу. Обозначим действующий в этом сечении изгибающий момент 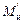 ,а момент сопротивления
,а момент сопротивления 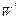 .Тогда должно выполняться условие
.Тогда должно выполняться условие
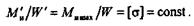
Отсюда следует, что в балках равного сопротивления изгибу моменты сопротивления сечений должны быть прямо пропорциональны изгибающим моментам:
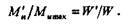
Изготовление балок равного сопротивления сложно в технологическом отношении, поэтому применение их ограничено.
|
Рассмотрим пример, иллюстрирующий теорию балок равного сопротивления изгибу.
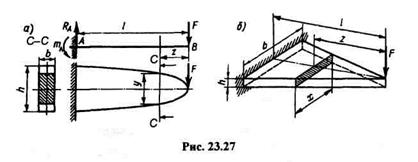
Пусть балка АВ прямоугольного сечения жестко защемлена одним концом, а к другому концу ее приложена сосредоточенная сила F,как показано на рис. 23.27, а.При условии равного сопротивления изгибу по всей длине установим: 1) как должна меняться высота h балки при постоянной ширине b;2) как должна меняться ширина балки при постоянной высоте.
1. Ширина балки постоянна. Изгибающий момент в произвольном сечении, отстоящем на расстоянии г от свободного конца,
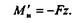
|
Соответствующий момент сопротивления
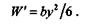
Здесь b = const, a y — меняется.
Максимальный изгибающий момент будет в защемлении:
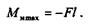
Момент сопротивления изгибу в защемлении
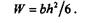
Запишем условие пропорциональности изгибающих моментов и моментов сопротивления изгибу:
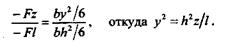
Это уравнение параболы. Заметим, что объем такой балки равного сопротивления изгибу будет составлять 2/3 объема балки постоянного сечения
b 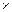 h,что дает экономию материала в 33% (рис. 23.27, б).
h,что дает экономию материала в 33% (рис. 23.27, б).
2. Высота балки постоянна.Обозначим переменную ширину х, ширину балки в защемлении b, высоту балки h.Как и в предыдущем случае, запишем

Из этого соотношения видно, что ширина балки изменяется по линейному закону. Подобная балка изображена на рис. 23.27, б.По сравнению с призматической балкой постоянного сечения экономия материала достигает 50%.
Сравним прогибы балок постоянного сечения и равного сопротивления изгибу при одинаковой прочности и прочих равных условиях.
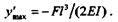
|
| Сравнивая это значение прогиба с прогибом свободного конца балки постоянного сечения |
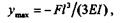
|
Формула для вычисления прогиба свободного конца балки равного сопротивления изгибу (без вывода)
приходим к выводу, что наибольший прогиб балки равного сопротивления изгибу в 1,5 раза превосходит прогиб балки постоянного сечения.
Свойство балок равного сопротивления изгибу (с постоянной высотой) деформироваться значительно больше балок постоянного сечения (при тех же нагрузках и допускаемых напряжениях) используется в случаях, когда необходимо смягчить действие нагрузки, изменяющейся с течением времени, или ударной нагрузки. В частности, листовые рессоры, широко применяющиеся на транспорте (вагоны, автомашины), представляют собой разрезанные на полосы и сложенные стопкой балки равного сопротивления изгибу.
Косой изгиб
До настоящего параграфа мы рассматривали прямой изгиб балок, при котором все нагрузки действовали в одной плоскости, проходящей через одну из главных осей сечения. При таком изгибе деформация оси балки происходит в плоскости действия нагрузок.
Изгиб, при котором плоскость действия нагрузок не совпадает ни с одной из главных осей сечения, называется косым.
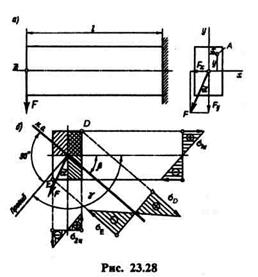
Рассмотрим консольную балку длиной l прямоугольного сечения, к концу которой приложена сила F,составляющая с осью у угол  (рис. 23.28, а).Разложим силу F на две составляющие, направленные по главным осям сечения, и, пользуясь принципом независимости действия сил, сведем косой изгиб к прямым изгибам в двух взаимно перпендикулярных
(рис. 23.28, а).Разложим силу F на две составляющие, направленные по главным осям сечения, и, пользуясь принципом независимости действия сил, сведем косой изгиб к прямым изгибам в двух взаимно перпендикулярных
|
плоскостях. Очевидно, что опасное сечение будет находиться в заделке и максимальные изгибающие моменты таковы:
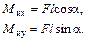
Соответствующие этим изгибающим моментам нормальные напряжения в какой-то точке А опасного сечения вычисляют по формулам
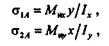
где х, у — текущие координаты точки А; Ix, Iу — моменты инерции относительно главных осей.
Суммарное нормальное напряжение в точке А
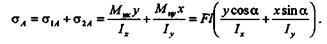
|
Если заштриховать в разные стороны части сечения, где будут действовать только напряжения растяжения 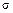 1и и
1и и 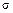 2и, то увидим, что в зоне, заштрихованной в клетку, будут действовать суммарные напряжения растяжения, а в незаштрихованной — суммарные напряжения сжатия (рис. 23.28, б).Очевидно, что максимальное напряжение растяжения возникает в точке D,а максимальное напряжение сжатия в точке Е опасного сечения. Эпюры нормальных напряжений показаны на том же рисунке.
2и, то увидим, что в зоне, заштрихованной в клетку, будут действовать суммарные напряжения растяжения, а в незаштрихованной — суммарные напряжения сжатия (рис. 23.28, б).Очевидно, что максимальное напряжение растяжения возникает в точке D,а максимальное напряжение сжатия в точке Е опасного сечения. Эпюры нормальных напряжений показаны на том же рисунке.
Так как на нейтральной оси 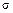 А = 0, то ее уравнение имеет вид
А = 0, то ее уравнение имеет вид
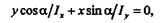
|
где х, у — текущие координаты точек нейтральной оси.
Из уравнения видно, что нейтральная ось есть прямая линия, проходящая через начало координат, т. е. через центр тяжести сечения балки. Определим угол 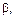 который нейтральная ось составляет с осью х:
который нейтральная ось составляет с осью х:
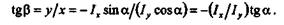
Из этого равенства видно, что если Ix  Iуто
Iуто 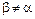 и нейтральная ось не перпендикулярна линии действия силы F.
и нейтральная ось не перпендикулярна линии действия силы F.
Пользуясь принципом независимости действия сил, определим направление прогиба балки под действием силы F. Прогиб fx в направлении оси хравен
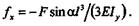
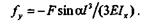
|
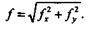
|
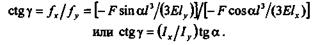
|
| Прогиб fy в направлении оси у будет |
| Суммарный прогиб f определится по формуле |
Обозначив 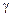 угол между направлением суммарного прогиба и осью х, получим угол между направлением суммарного прогиба и осью х, получим
|
Сравнивая это выражение с формулой для определения tg 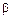 , видим, что ctg
, видим, что ctg 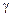 и tg
и tg 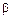 отличаются только знаком, следовательно, сами углы разнятся на 90° и суммарный прогиб балки происходит в плоскости, перпендикулярной нейтральной оси. Отсюда вытекает, что при косом изгибе плоскость прогиба не совпадает с плоскостью действия нагрузок.
отличаются только знаком, следовательно, сами углы разнятся на 90° и суммарный прогиб балки происходит в плоскости, перпендикулярной нейтральной оси. Отсюда вытекает, что при косом изгибе плоскость прогиба не совпадает с плоскостью действия нагрузок.
Глава 24
Дата добавления: 2021-09-07; просмотров: 980;











