Силы инерции в криволинейном движении
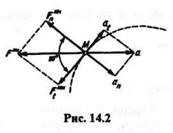
В криволинейном движении точки полное ускорение равно векторной сумме касательного и нормального ускорений (рис. 14.2).
 Касательное ускорение
Касательное ускорение 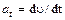 , нормальное ускорение аn =
, нормальное ускорение аn = 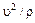 , полное ускорение
, полное ускорение
|
Каждому ускорению соответствует своя сила инерции:
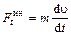 —касательная, или тангенциальная;
—касательная, или тангенциальная;
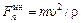 —нормальная, или центробежная;
—нормальная, или центробежная;
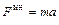 — полная.
— полная.
В качестве примера рассмотрим равномерное движение по окружности, лежащей в горизонтальной плоскости, камня силой тяжести G,привязанного к невесомой нити длиной r, расположенной в той же плоскости (рис. 14.3, а).Чтобы нить оставалась в плоскости движения камня, предполагается, что он скользит по идеальной гладкой горизонтальной плоскости. Скорость камня обозначим 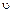 . Тогда
. Тогда 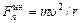 — центробежная сила инерции (эта сила натягивает нить);
— центробежная сила инерции (эта сила натягивает нить); 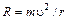 — центростремительная сила, приложенная к камню (эта сила удерживает камень на окружности).
— центростремительная сила, приложенная к камню (эта сила удерживает камень на окружности).
Центробежная и центростремительная силы (действие и противодействие) по третьему закону Ньютона равны по модулю и направлены в противоположные стороны. Очевидно, что касательная сила инерции
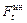 в этом случае равна нулю, так как
в этом случае равна нулю, так как 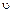 = const.
= const.
Из опыта известно, что при достаточной скорости нить может разорваться и камень полетит по касательной к окружности, т. е. по направлению имеющейся в момент разрыва скорости. Это доказывает, что центробежная сила инерции есть реальная сила для связи, но к телу она приложена условно.
Внутри тел, движущихся с ускорением, также возникают внутренние силы инерции, так как для каждой частицы тела соседние частицы являются связями.
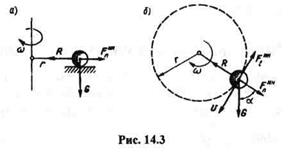
Найдем, чему равно натяжение нити, если камень движется по окружности, лежащей в вертикальной плоскости (рис. 14.3, б). Для определения натяжения R нити применим принцип Даламбера, т. е. приложим к
камню нормальную силу инерции 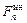 и касательную силу инерции
и касательную силу инерции 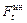 .
.
Спроецируем все силы на направление нити, в результате чего получим
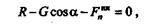
откуда
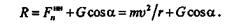
|
Натяжение нити максимальное при  = 0, т. е. когда камень находится в нижнем положении:
= 0, т. е. когда камень находится в нижнем положении:
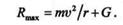
|
Натяжение нити минимальное при  =
= 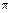 рад, т. е. когда камень находится в верхнем положении:
рад, т. е. когда камень находится в верхнем положении:
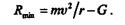
Заметим, что под влиянием силы тяжести камня модуль его скорости w будет меняться и достигать наименьшего значения в верхнем положении и наибольшего — в нижнем.
Если выразить линейную скорость камня через угловую скорость нити
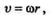
|
то формула центробежной силы инерции примет вид
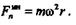
|
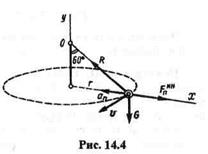
Пример 14.2. Груз G = 10 Н, подвешенный на нити длиной l = 0,3 м в неподвижной точке О, представляет собой конический маятник, т. е. описывает окружность в горизонтальной плоскости, причем нить составляет с вертикалью угол 60° (рис. 14.4). Определить скорость 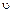 груза и натяжение R нити.
груза и натяжение R нити.
|
Решение. Так как нить составляет с вертикалью постоянный угол, то скорость груза постоянна, касательное ускорение груза и касательная сила инерции равны нулю. Применим принцип Даламбера, т. е. приложим к грузу центробежную силу инерции 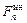 , реакцию R нити и составим два уравнения равновесия:
, реакцию R нити и составим два уравнения равновесия:

где
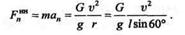
Из второго уравнения определим
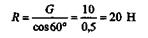
|
и подставим в первое уравнение
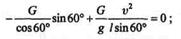
отсюда
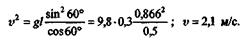
Пример 14.3.Определить скорость 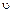 искусственного спутника Земли, движущегося по круговой орбите на высоте h = 230 км от поверхности Земли. Изменением ускорения свободного падения и сопротивлением воздуха пренебречь. Радиус Земли считать равным R = 6370 км.
искусственного спутника Земли, движущегося по круговой орбите на высоте h = 230 км от поверхности Земли. Изменением ускорения свободного падения и сопротивлением воздуха пренебречь. Радиус Земли считать равным R = 6370 км.
Решение. После того как ракета-носитель вывела спутник массой т на заданную орбиту и сообщила ему скорость 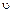 ,касательную к орбите, спутник продолжает движение под действием одной лишь силы притяжения Земли. Для определения скорости v спутника применим принцип Даламбера, т. е. приложим к спутнику центробежную силу инерции и составим уравнение равновесия, спроецировав силы на ось, проходящую через спутник и центр Земли:
,касательную к орбите, спутник продолжает движение под действием одной лишь силы притяжения Земли. Для определения скорости v спутника применим принцип Даламбера, т. е. приложим к спутнику центробежную силу инерции и составим уравнение равновесия, спроецировав силы на ось, проходящую через спутник и центр Земли:
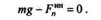
|
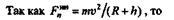
|
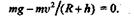
Сократив равенство на т, определим скорость спутника:
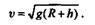
|
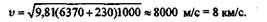
|
| Подставив значения, получим |
Эта скорость, при которой спутник Земли удерживается на круговой орбите на относительно небольшой высоте, называется первой космической скоростью.
Пример 14.4.На какую высоту h надо запустить искусственный спутник Земли, предназначенный для сверхдальних телепередач, чтобы он казался неподвижным по отношению к Земле? Орбиту спутника приближенно считать окружностью, концентричной экватору.
Радиус R Земли принять равным 6370 км, а угловую скорость вращения Земли вокруг своей оси 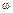 = 0,7
= 0,7  10-4 рад/с (рис. 14.5).
10-4 рад/с (рис. 14.5).
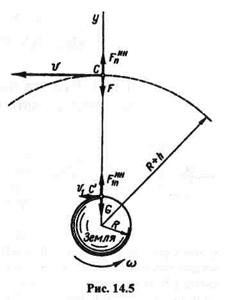
|
Решение. Введем следующие обозначения: т — масса спутника; G — сипа тяжести спутника на поверхности Земли; М— масса Земли; 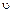 — скорость движения спутника.
— скорость движения спутника.
На основании закона всемирного тяготения сила F,с которой спутник притягивается к Земле, на высоте h равна
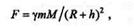
где 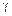 — гравитационная постоянная. При h = 0
— гравитационная постоянная. При h = 0
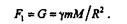
Центробежная сила инерции 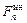 спутника на высоте h равна
спутника на высоте h равна
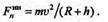
На основании принципа Далам-бера
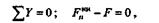
следовательно,
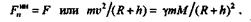
Так как v = 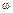 (R + h),то после подстановки и сокращений получим
(R + h),то после подстановки и сокращений получим
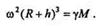 (14.1)
(14.1)
Если бы спутник летел на небольшом расстоянии от поверхности Земли, то этим расстоянием можно было бы пренебречь и тогда
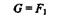
|
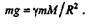
|
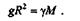
|
или
Отсюда
(14.2)
Из равенств (14.1) и (14.2) получим
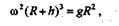
откуда
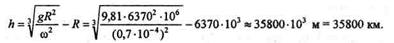
Глава 15
РАБОТА И МОЩНОСТЬ
Дата добавления: 2021-09-07; просмотров: 583;











