Аналитические условия равновесия
Пространственной системы произвольно
Расположенных сил
Строгое обоснование условий равновесия пространственной системы произвольно расположенных сил требует знания некоторых вопросов, не предусматриваемых программами средних специальных учебных заведений, поэтому примем эти условия без доказательства.
Для равновесия пространственной системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из трех осей координат была равна нулю и чтобы алгебраическая сумма моментов всех сил относительно каждой из этих осей была равна нулю.
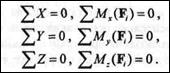
|
| Поясним смысл этих условий, для чего применим три условия равновесия плоской системы произвольно расположенных сил: |
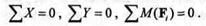
|
Запишем условия равновесия:
Тело, лежащее на плоскости, имеет три степени свободы, а именно: возможность перемещения в направлениях двух взаимно перпендикулярных осей, лежащих в этой плоскости, и возможность вращения вокруг оси, перпендикулярной этой плоскости. Если к телу приложена плоская система сил и выполнено условие 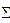 X = 0, то тело не будет перемещаться в направлении оси х, так как равнодействующая системы не имеет составляющей, параллельной оси х. Если выполнено условие
X = 0, то тело не будет перемещаться в направлении оси х, так как равнодействующая системы не имеет составляющей, параллельной оси х. Если выполнено условие 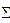 Y = 0, то тело не будет перемещаться и в направлении оси у, так как равнодействующая системы не имеет составляющей, параллельной оси у. Наконец, если выполнено условие
Y = 0, то тело не будет перемещаться и в направлении оси у, так как равнодействующая системы не имеет составляющей, параллельной оси у. Наконец, если выполнено условие 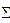 M (Fi) = 0, т.е. сумма моментов относительно любой точки
M (Fi) = 0, т.е. сумма моментов относительно любой точки
плоскости равна нулю, то тело не будет под действием этой системы сил вращаться, так как нет пары сил, которая может осуществить это вращение.
Таким образом, трем степеням свободы тела на плоскости соответствуют три условия равновесия.
Свободное тело в пространстве имеет шесть степеней свободы, а именно: возможность перемещаться в направлениях трех взаимно перпендикулярных осей координат и возможность вращаться вокруг этих осей. Таким образом, шести степеням свободы тела в пространстве соответствуют шесть условий равновесия.
Если система сил, приложенная к свободному телу, удовлетворяет всем шести условиям равновесия, то возможность трех перемещений и грех вращений под действием этой системы исключена и тело будет находиться в равновесии.
Нетрудно показать, что все выведенные выше условия равновесия для различных систем сил являются частными случаями условий равновесия, рассмотренных здесь.
В случае, если на свободное тело действует пространственная система параллельных сил (например, параллельных оси z),то условия равновесия этой системы запишутся так:
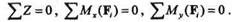
|
Остальные три условия равновесия будут представлять собой тождества, так как проекции всех сил такой системы на оси х и у равны нулю и моменты всех сил относительно оси z также равны нулю.
Так как условия равновесия пространственной системы сил справедливы для любых прямоугольных осей координат, то при решении данной задачи систему координат можно изменять, т. е. часть условий равновесия составить для одних осей координат, а часть — для измененных.
Кроме того, можно одно, два или все три уравнения проекций сил заменить уравнениями моментов сил относительно новых осей координат (см. пример 7.2). В некоторых случаях такие приемы упрощают решение задач.
При решении задач уравнения моментов сил относительно осей в общем виде будем записывать упрощенно, а именно:
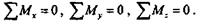
|
Пример 7.2. На горизонтальном валу АВ (рис. 7.6) насажены зубчатое колесо 1 диаметром D = 2 м и шестерня 2 диаметром d = 20 см. Остальные размеры указаны на рисунке. К колесу 1 по касательной приложена горизонтальная сила Р = 100 Н, а к шестерне 2 также по касательной приложена вертикальная сила Q. Определить силу Q и реакции подшипников А и В в положении равновесия. Массой деталей пренебречь.
Решение. Отбросим подшипники и рассмотрим равновесие вала с зубчатым колесом и шестерней. Реакции подшипников А и В перпендикулярны оси вала. Поэтому разложим каждую из этих реакций на две взаимно перпендикулярные
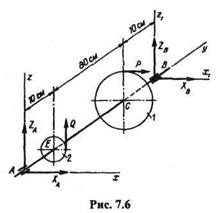
|
составляющие, параллельные осям координат х и z. В результате получена приложенная к заданной системе тел пространственная система шести сил, пять из которых, т. е. ХA, ZA, XB, ZB, Q, не известны по модулю.
Применим условия равновесия пространственной системы произвольно расположенных сил и составим пять уравнений равновесия:
1) 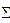 Мy= 0; -Qd/2 + PD/2 = 0.
Мy= 0; -Qd/2 + PD/2 = 0.
Из этого уравнения
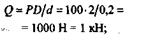
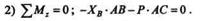
Из этого уравнения
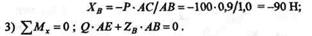
Из этого уравнения
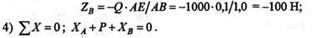
Из этого уравнения
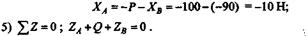
Из этого уравнения
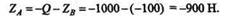
Знак «-» перед значениями реакций ХA, ХB, ZА и ZB показывает, что эти реакции направлены противоположно указанным на рисунке.
Шестое условие равновесия 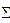 Y = 0 обращается в тождество, так как проекции на ось у всех сил рассматриваемой системы равны нулю.
Y = 0 обращается в тождество, так как проекции на ось у всех сил рассматриваемой системы равны нулю.
Для проверки решения составим дополнительное, контрольное уравнение моментов относительно оси хь проходящей через точку В:
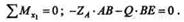
Подставив значения, получим 900  1,0 - 1000
1,0 - 1000  0,9 = 0.
0,9 = 0.
Контрольное уравнение обращается в тождество, что свидетельствует о правильности полученных ответов.
На этом примере покажем возможность изменения при решении системы координатных осей и замены уравнения проекций уравнением моментов.
Определим реакцию ХA, составив вместо уравнения проекций сил на ось х уравнение моментов сил относительно новой оси z1, проходящей через точку В:
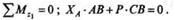
Из этого уравнения
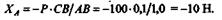
Как видим, ответ получен тот же.
Дата добавления: 2021-09-07; просмотров: 763;











