Разложение силы по трем осям координат
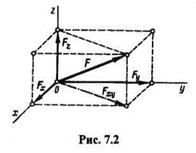
Пусть дана сила F(рис. 7.2). Возьмем систему координат так, чтобы начало координат совпадало с началом вектора силы F. Из конца этого
|
|
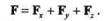
|
| вектора опустим перпендикуляр на плоскость ху и разложим силу F на составляющие Fxy и Fz, а составляющую Fxy — на составляющие Fx и Fу.Тогда |
Достроим полученное изображение до параллелепипеда, у которого составляющие Fx, Fy, Fz являются ребрами, а сила F — диагональю.
Из изложенного можно сделать такой вывод: равнодействующая трех взаимно перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах.
Из рис. 7.2 видно, что в случаях разложения силы F по трем взаимно перпендикулярным направлениям х, у, z составляющие Fx, Fy, Fz равны по модулю проекциям силы F на эти оси. Эти проекции обозначим Fx, Fy, Fz.
Зная проекции силы на три взаимно перпендикулярные оси координат, можно определить модуль и направление вектора силы по формулам:
модуль силы
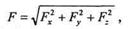
направляющие косинусы
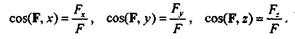
Аналитический способ определения
Дата добавления: 2021-09-07; просмотров: 691;











