Пространственной системы сходящихся сил
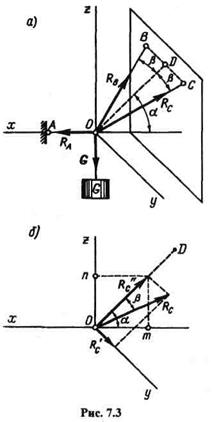
Известно, что пространственная система сходящихся сил эквивалентна равнодействующей. Если такая система находится в равновесии, т. е. эквивалентна нулю, то равнодействующая этой системы равна нулю, а следовательно, и проекции равнодействующей равны нулю, причем эти проекции равны сумме проекций составляющих.
|
Отсюда вытекают условия равновесия пространственной системы сходящихся сил:
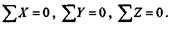
Эти условия формулируются следующим образом: для равновесия пространственной системы сходящихся сил необходимо и достаточн  о, чтобы алгебраическая сумма проекций всех сил на каждую из трех координатных осей равнялась нулю.
о, чтобы алгебраическая сумма проекций всех сил на каждую из трех координатных осей равнялась нулю.
Пример 7.1. Груз G = 200 Н удерживается в равновесии горизонтальной веревкой АО и двумя веревками ВО и СО,плоскость которых наклонена к горизонтальной плоскости под углом 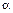 =45° и образует с вертикальной плоскостью, проходящей через АО, прямой угол (рис. 7.3, а).Веревки ВО и СО образуют с этой вертикальной плоскостью углы
=45° и образует с вертикальной плоскостью, проходящей через АО, прямой угол (рис. 7.3, а).Веревки ВО и СО образуют с этой вертикальной плоскостью углы 
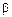 = 30°. Определить натяжение веревок.
= 30°. Определить натяжение веревок.
Решение. Рассмотрим равновесие узла О,к которому приложены четыре силы: G, RA, RB, RC. К пространствен-
ной системе четырех сходящихся сил применим аналитические условия равновесия и составим три уравнения равновесия:
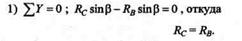
Так как углы между реакциями RB, RC и осями координат х и z неизвестны, то для удобства проецирования каждую из этих сил разложим на две составляющие, как показано на рис. 7.3, б.Тогда
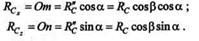
Проекции составляющей 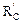 на оси х и z равны нулю, так как эта составляющая перпендикулярна указанным осям;
на оси х и z равны нулю, так как эта составляющая перпендикулярна указанным осям;
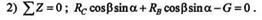
Учитывая, что RВ=RC,получаем
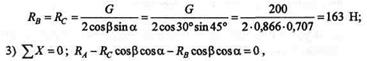
откуда
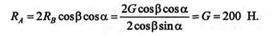
|
Дата добавления: 2021-09-07; просмотров: 545;











