Пространственная система сходящихся сил

Система сил, линии действия которых расположены в различных плоскостях, называется пространственной системой сил.

Пространственная система сил называется сходящейся, если ли­нии действия всех сил системы пересекаются в одной тЪчке.

Теорема. Пространственная система сходящихся сил эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.

Пусть дана пространственная система п сходящихся сил (F₁, F₂, F₃ ..., F_n). На основании следствия из аксиом III и IV перенесем все силы системы вдоль линий действия в точку их пересечения. Затем на основа­нии аксиомы параллелограмма сложим силы F₁ и F₂, в результате чего получим их равнодействующую:

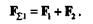
Сложив эту равнодействующую с силой F₃, получим равнодейст­вующую трех сил:

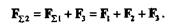
Повторив указанную операцию п - 1 раз, получим равнодействую­щую системы п сил, которая будет равна векторной сумме этих сил; ли­ния действия равнодействующей будет проходить через точку пересече­ния линий действия составляющих:

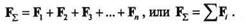
Силовой многоугольник пространственной системы сил не лежит в одной плоскости, поэтому геометрический и графический способы нахо­ждения равнодействующей неприемлемы, а применяется аналитиче­ский способ (методпроекций).