Разложение силы на две составляющие
Разложить силу на составляющие — это значит найти систему сил, эквивалентную данной силе. В общем случае задача разложения силы на две составляющие есть задача неопределенная, имеющая бесчисленное множество решений. Для того чтобы задача имела определенное решение, необходимо задать два условия, например направления или модули двух составляющих и т. п. Возможны четыре варианта разложения силы F 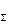 на две составляющие Р и Q, приложенные в той же точке. Во всех
на две составляющие Р и Q, приложенные в той же точке. Во всех
случаях решение сводится к построению параллелограмма сил.
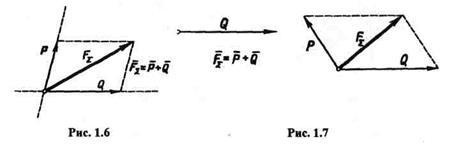
1. Даны направления двух составляющих Р и Q.
Решение показано на рис. 1.6.
2. Даны модуль и направление одной составляющей Q.
Решение показано на рис. 1.7
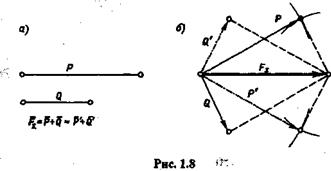
3. Даны модули двух составляющих Р и Q.
Задача решается методом засечек (рис. 1.8).
Задача имеет два решения, если Р + Q> F 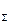 и P-Q< F
и P-Q< F 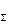 .
.
|
|
Задача не имеет решений, если Р + Q> F 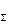 и P-Q> F
и P-Q> F 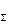 . Задача имеет одно решение, если Р + Q> F
. Задача имеет одно решение, если Р + Q> F 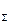 и P-Q= F
и P-Q= F 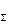 .
.
|
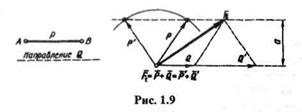
4. Даны направление составляющей Q и модуль второй составляющей Р.
Задача решается методом засечек (рис. 1.9).
Задача имеет одно решение, если а =АВ (в этом случае угол между векторами Р и Q равен 90°).
Задача имеет два решения, если а < АВ.
Задача не имеет решений, если а > АВ.
Из рис. 1.9 видно, что модуль составляющей зависит от направления второй составляющей.
|
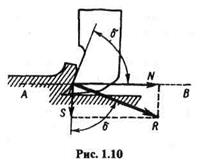
Пример 1.1. Сипа давления пружки по направлению, перпендикулярному передней грани резца, равна R.Угол резания резца (угол между передней гранью и направлением движения обрабатываемой детали) равен 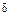 . Определить силу N сопротивления резанию, направленную по линии АВ,и перпендикулярную ей силу S,прижимающую резец к обрабатываемой поверхности (рис 1.10). Трением пренебречь.
. Определить силу N сопротивления резанию, направленную по линии АВ,и перпендикулярную ей силу S,прижимающую резец к обрабатываемой поверхности (рис 1.10). Трением пренебречь.
Решение. Разложим заданную силу R на две составляющие N и S по заданным направлениям. Из прямоугольного треугольника получим
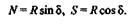
Дата добавления: 2021-09-07; просмотров: 607;











