Прочность, жесткость, устойчивость

Прочность, жесткость, устойчивость, – как понятия определяющие надёжность конструкций в их сопротивлении внешним воздействиям. Расчётные схемы (модели): твёрдого деформируемого тела, геометрических форм элементов конструкций. Внутренние силы в деформируемых телах и их количественные меры. Метод сечений. Напряжённое состояние. Перемещения и деформации. Понятия упругости и пластичности. Линейная упругость (закон Гука). Принцип независимости действия сил (принцип суперпозиции).

Основные понятия. Сопротивление материалов, наука о прочности (способности сопротивляться разрушению при действии сил) и деформируемости (изменении формы и размеров) элементов конструкций сооружений и деталей машин. Таким образом, данный раздел механики дает теоретические основы расчета прочности, жесткости и устойчивости инженерных конструкций.

Под нарушением прочности понимается не только разрушение конструкции, но и возникновение в ней больших пластических деформаций. Пластическая деформация – это часть деформации, которая не исчезает при разгрузке, а пластичность - способность материала сохранять деформацию.

Жесткость – это способность конструкции (или материала) сопротивляться деформированию.

Устойчивость – это способность конструкции сохранять положение равновесия, отвечающее действующей на нее нагрузке.

Надежность – свойство конструкции выполнять заданные функции, сохраняя свои эксплуатационные показатели в определенных нормативных пределах в течение требуемого промежутка времени.

Ресурс – допустимый срок службы изделия. Указывается в виде общего времени наработки или числа циклов нагружения конструкции.

Отказ – нарушение работоспособности конструкции.

Опираясь на вышесказанное, можно дать определение прочностной надежности.

Прочностной надежностью называется отсутствие отказов, связанных с разрушением или недопустимыми деформациями элементов конструкции.

Конструкции, как правило, имеют сложную форму, отдельные элементы которой можно свести к простейшим типам, являющимися основными объектами изучения сопротивления материалов: стержни, пластинки, оболочки, массивы, для которых устанавливаются соответствующие методы расчёта на прочность, жёсткость и устойчивость при действии статических и динамических нагрузок, т.е. расчет реальной конструкции начинается с выбора расчетной схемы.

Выбор расчетной схемы начинается со схематизации свойств материала и характера деформирования твердого тела, затем выполняется схематизация геометрической.

Стержень – тело, у которого один размер (длина) значительно превышает два других размера.

Оболочка – это тело, ограниченное двумя криволинейными поверхностями, у которого один размер (толщина) много меньше двух других размеров. Пластина – это тело, ограниченное двумя параллельными плоскостями.

Массив– тело, у которого все три размера имеют один порядок .

Базируясь на законах и выводах теоретической механики, сопротивление материалов, помимо этого, учитывает способность реальных материалов деформироваться под действием внешних сил.

При выполнении расчетов принимаются допущения, связанные со свойствами материалов и с деформацией тела.

Основные допущения.

1. Материал считается однородным (независимо от его микроструктуры физико-механические свойства считаются одинаковыми во всех точках).

2. Материал полностью заполняет весь объем тела, без каких-либо пустот (тело рассматривается как сплошная среда).

3. Обычно сплошная среда принимается изотропной, т.е. пред­полагается, что свойства тела, выделенного из нее, не зависят от его ориентации в пределах этой среды. Материалы, имеющие различные свойства в разных направлениях, называют анизотропными (например, дерево).

4. Материал является идеально упругим (после снятия нагрузки все деформации полностью исчезают, т.е. геометрические размеры тела полностью или частично восстанавливаются). Свойство тела восстанавливать свои первоначальные размеры после разгрузки называется упругостью.

5. Деформации тела считаются малыми по сравнению с его размерами. Это допущение называется принципом начальных размеров. Допущение позволяет при составлении уравнений равновесия пренебречь изменениями формы и размеров конструкции.

6. Перемещения точек тела пропорциональны нагрузкам, вызывающим эти перемещения (до определенной величины деформации материалов подчиняются закону Гука). Для линейно деформируемых конструкций справедлив принцип независимости действия сил (или принцип суперпозиции): результат действия группы сил не зависит от последовательности нагружения ими конструкции и равен сумме результатов действия каждой из этих сил в отдельности.

7. Предполагается, что в сечениях, достаточно удаленных от мест приложения нагрузки, характер распределения напряжений не зависит от конкретного способа нагружения. Основанием для такого утверждения служит принцип Сен-Венана.

8.Принимается гипотеза плоских сечений (гипотеза Бернулли): плоские поперечные сечения стержня до деформации остаются плоскими и после деформации.

Внутри любого материала имеются внутренние межатомные силы. При деформации тела изменяются расстояния между его частицами, что в свою очередь приводит к изменению сил взаимного притяжения между ними. Отсюда, как следствие, возникают внутренние усилия. Для определения внутренних усилий используют метод сечения. Для этого тело мысленно рассекают плоскостью и рассматривают равновесие одной из его частей (рис.1).

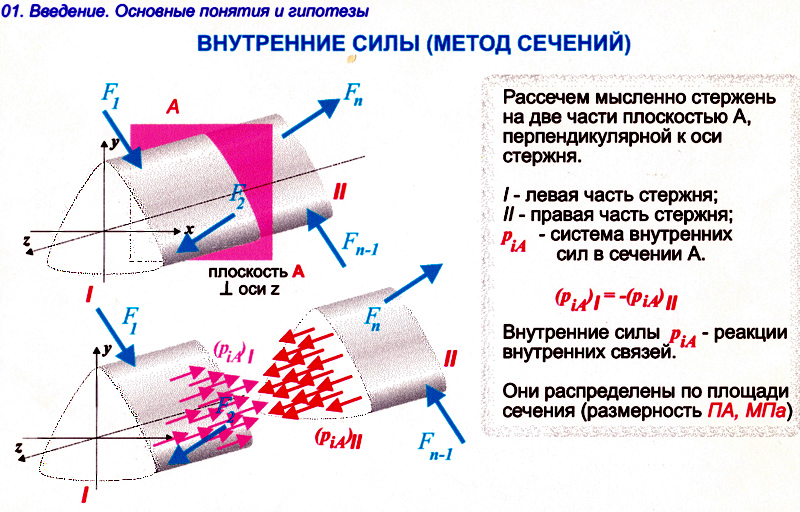
Рис.1

Метод заключается в следующем: 1. Разрезаем систему (на части); 2.Отбрасываем одну часть; 3. Заменяем действие отброшенной части на оставшуюся внутренними силами упругости (приложим в сечении усилия, способные уравновесить внешние силы, действующие на отсеченную часть); 4. Составляем уравнения равновесия, составленное для отсеченной части и находим значения усилий.

Используем метод сечений и приведем внутренние силы к центру тяжести поперечного сечения стержня. В результате приведения мы получим результирующую силу 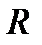, равную главному вектору и пару сил с моментом 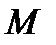, равным главному моменту системы.

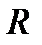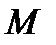Проектируя и на координатные оси, получаем в общем случае 6 алгебраических величин - 6 внутренних силовых факторов: 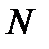- нормальная сила; Q _y или Q _z- поперечные силы; M _y или M _z - изгибающие моменты; 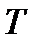- крутящий момент.