Моменты инерции относительно параллельных осей.
При рассмотрении нескольких осей, параллельных друг другу (рис.4), оказывается, что можно легко вычислить моменты инерции фигуры относительно любой из этих осей, зная ее момент инерции относительно оси, проходящей через центр тяжести фигуры параллельно выбранным осям.
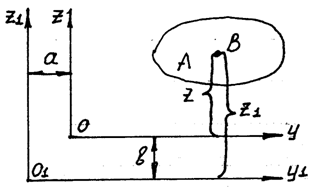
Рис.4.
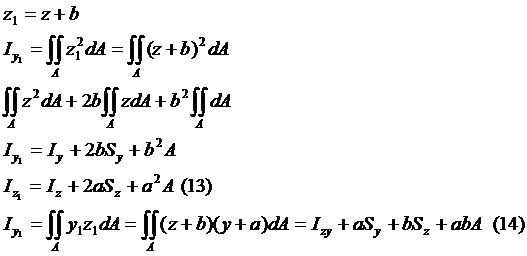 Рассмотрим произвольную фигуру. Проведем центральную ось Оу, момент инерции относительно этой оси назовем
Рассмотрим произвольную фигуру. Проведем центральную ось Оу, момент инерции относительно этой оси назовем 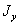 . Проведем в плоскости фигуры ось
. Проведем в плоскости фигуры ось 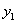 параллельно оси у на расстоянии
параллельно оси у на расстоянии 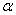 от нее. Найдем зависимость между
от нее. Найдем зависимость между 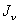 и
и 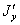 — моментом инерции относительно оси
— моментом инерции относительно оси 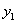 . Для этого напишем выражения для
. Для этого напишем выражения для 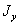 и
и 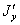 . Разобьем площадь фигуры на площадки dA; расстояния каждой такой площадки до осей у и
. Разобьем площадь фигуры на площадки dA; расстояния каждой такой площадки до осей у и 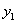 назовем
назовем 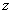 и
и 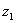 . Тогда из рис.4 имеем:
. Тогда из рис.4 имеем:
Первый из этих трех интегралов — момент инерции относительно оси Оу. 2-ой — статический момент относительно той же оси; 3-й интеграл – площадь.
Так как ось Оу – центральная, то второе слагаемое— статический момент относительно той же оси равен нулю, так как ось у проходит через центр тяжести фигуры.
Таким образом,
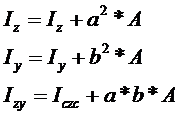 ,
,
т. е. осевой момент инерции относительно любой оси равен моменту инерции относительно центральной оси, проведенной параллельно у данной, плюс произведение площади фигуры на квадрат расстояния между осями; а центробежный момент инерции относительно системы взаимно перпендикулярных осей, параллельных центральным, равен центробежному моменту инерции относительно этих центральных осей плюс произведение из площади фигуры, на координаты ее центра тяжести относительно новых осей.
Зависимость между моментами инерции при повороте осей.
Центральных осей можно провести сколько угодно. Является вопрос, нельзя ли выразить момент инерции относительно любой центральной оси в зависимости от момента инерции относительно одной или двух определенных осей. Для этого посмотрим, как будут меняться моменты инерции относительно двух взаимно перпендикулярных осей при повороте их на угол 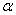 .
.
Возьмем какую-либо фигуру и проведем через ее центр тяжести О две взаимно перпендикулярные оси Оу и Oz (рис.2).
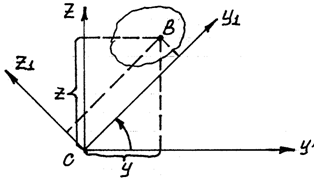
Рис.2. Расчетная модель для определения моментов инерции для повернутых осей.
Пусть нам известны осевые моменты инерции относительно этих осей 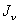 ,
, 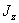 , а также центробежный момент инерции
, а также центробежный момент инерции 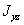 .Начертим вторую систему координатных осей
.Начертим вторую систему координатных осей 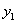 и
и 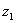 наклоненных к первым под углом
наклоненных к первым под углом 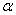 ; положительное направление этого угла будем считать при повороте осей вокруг точки О против часовой стрелки. Начало координат О сохраняем. Выразим моменты относительно второй системы координатных осей
; положительное направление этого угла будем считать при повороте осей вокруг точки О против часовой стрелки. Начало координат О сохраняем. Выразим моменты относительно второй системы координатных осей 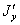 и
и 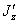 , через известные моменты инерции
, через известные моменты инерции 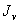 и
и 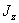 .
.
Напишем выражения для моментов инерции относительно этих осей.
Из чертежа видно, что координаты площадки dA в системе повернутых осей 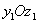 будут:
будут:
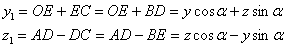 Подставляя эти значения
Подставляя эти значения 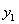 и
и 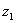 в (1), получим:
в (1), получим:
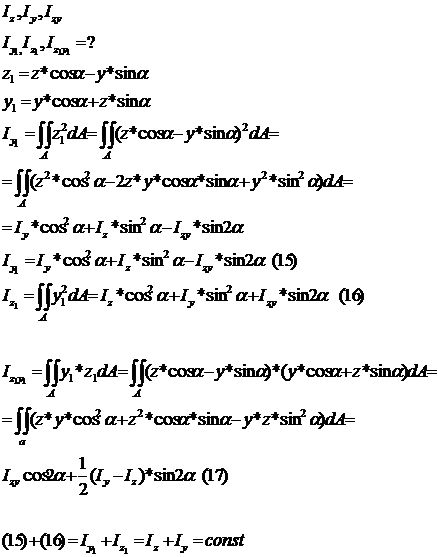
Также
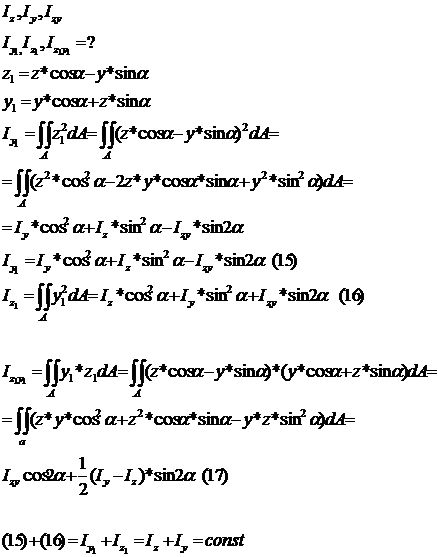
Моменты инерции при повороте осей изменяются, и при некотором угле α экстремальные значения достигают максимума.
Оси, относительно которых осевые моменты инерции принимают экстремальные значения, называются главными осями инерции.
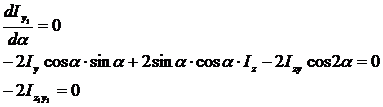
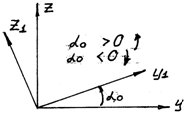
Относительно главных осей центробежный момент равен нулю. Оси, проходящие через центры тяжести, называются главными центральными осями.
Положение главных осей:
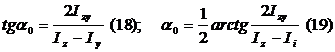
Значения главных центральных моментов инерции:
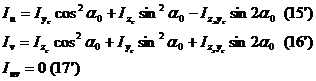
Дата добавления: 2017-09-01; просмотров: 2271;











