Лекция 4. Сдвиг (срез).

Понятие чистого сдвига. Элементы конструкций, работающих в условиях чистого сдвига. Деформации, напряжения. Площадки чистого сдвига. Закон Гука при сдвиге. Условие прочности при сдвиге (срезе).

Сдвиг (срез) - вид деформации, при котором одна часть стержня смещается относительно другой (скользит). Сдвиг, как вид нагружения, встречается редко и имеет место в заклепочных и сварных соединениях. Деформация сдвига происходит в случае, если к стержню приложены две равные по модулю противоположно направленные силы P , перпендикулярные к его продольной оси. Расстояние между этими силами должно быть малым, чтобы можно было пренебречь моментом, создаваемым силами.

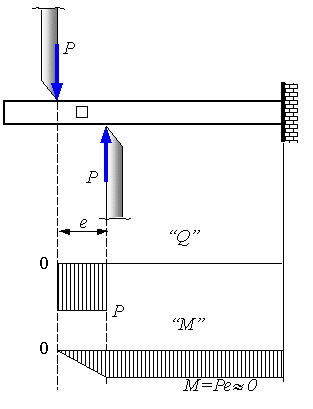
Используя метод сечений (разрезая стержень между силами P), можно установить, что в поперечном сечении стержня возникает только одно внутреннее усилие – поперечная сила Q.

Такой вид нагружения, при котором в поперечных сечениях стержня действует только поперечная сила, называют чистым сдвигом.

Мера скольжения одного поперечного сечения относительно другого - касательные напряжения τ.

Принято, что касательные напряжения распределены по всей площади поперечного сечения равномерно.

Рис.1

Если в поперечном сечении стержня площадью A возникает внутренняя поперечная сила Q=P , то касательные напряжения в любой точке этого сечения будут равны: Τ = Q / A = P / A.

При чистом сдвиге возникает плоское напряженное состояние, тогда напряжения, действующие на площадке составляющей угол 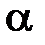с вертикальной исходной площадкой равны:

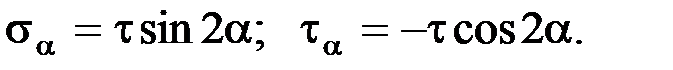
Касательные напряжения τ, приведенные на рис. 1, по абсолютной величине больше касательных напряжений по любым другим площадкам. Таким образом, они являются экстремальными, а площадки, по которым они действуют – площадками сдвига. Так как по этим площадкам не действуют нормальные напряжения, то их называют площадками чистого сдвига и они образуют с главными площадками углы, равные 45⁰.

При чистом сдвиге нормальные напряжения на любых двух взаимно перпендикулярных площадках равны друг другу по модулю и противоположны по направлению.

В результате сдвига одно поперечное сечение стержня смещается относительно другого на величину δ , называемую абсолютным сдвигом.

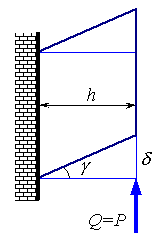
Малый угол γ, на который изменится первоначально прямой угол, – относительный сдвиг, выражается в радианах.

Угол сдвига 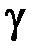пропорционален касательным напряжениям. Математическая зависимость между углом сдвига и касательным напряжением называется законом Гука при сдвиге:

.

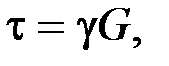Зависимость между модулем сдвига и модулем Юнга:

.

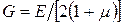Значение коэффициента Пуассона μ находится в пределах 0 ≤ μ ≤ 0,5.

Условие прочности при сдвиге имеет вид:

τ = Q / A ≤ [ τ ]

Кручение.

Крутящие моменты (внутренний силовой фактор) в поперечных сечениях стержня. Кручение стержней круглого поперечного сечения: допущения, деформации, напряжения, углы закручивания. Условия прочности, жёсткости. Построение эпюр крутящих моментов.

Кручение имеет место в случае действия на вал момента (пары сил) относительно его продольной оси, и в поперечных сечениях бруса возникает только один силовой фактор – крутящий момент. Брус, работающий на кручение называется валом. При кручении вала его поперечные сечения поворачиваются друг относительно друга, вращаясь вокруг оси бруса.

Напряжения и деформации при кручении бруса. Под действием внешнего скручивающего момента, приложенного на правом конце бруса, левый конец которого жестко закреплен, брус будет закручиваться. Выделим из бруса элементарный цилиндр длиной 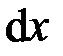. Будем считать, что левое сечение бруса жестко закреплено. Под действием крутящего момента 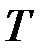правое сечение повернется на некоторый угол .

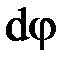Так как 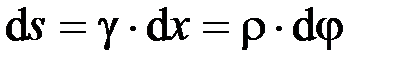, то получаем .

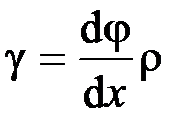Из данной зависимости видно, что угол сдвига 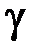изменяется по радиусу вала по линейному закону.

Деформация бруса при кручении характеризуется относительным углом закручивания .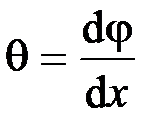

При малых углах закручивания вала в теории кручения круглых стержней принимаются допущения:

1. Поперечные сечения, плоские и перпендикулярные к его оси до деформации, остаются плоскими (не коробятся) и перпендикулярными к оси вала и после деформации (гипотеза Бернулли);

2. Радиусы поперечных сечений при деформации не искривляются и не изменяют своей длины;

3. Длина вала в результате закручивания не изменяется.

Поперечное сечение вала ведет себя при кручении, как жесткий диск, идеформациюкручения можно рассматривать, как результатсдвига одного поперечного сечения относительно другого. В этом случае в точках поперечного сечения вала возникают только касательные напряжения.

Теория кручения, основанная на упомянутых допущениях, подтверждается экспериментальными данными.

Согласно закону Гука при сдвиге, имеем 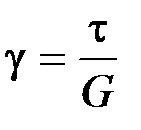. Откуда получаем: .

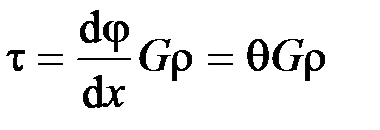Из полученной зависимости следует, что касательные напряжения изменяются по радиусу по линейному закону.

При кручении все внутренние силы, распределенные по поперечному сечению, приводятся к одной составляющей - к крутящему моменту. Крутящий момент 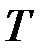в сечении бруса определяется по формуле

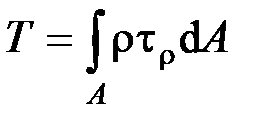, где 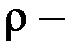плечо элементарной силы.

Подставляя значение касательного ускорения, получим

.

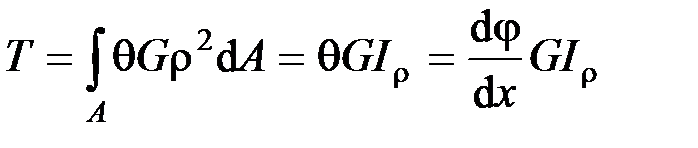Элементарный угол закручивания бруса: 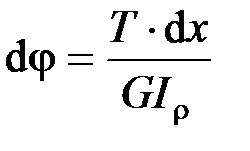; полный угол закручивания .

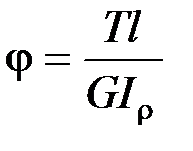Максимальное касательное напряжение в поперечном сечении бруса будет определяться по зависимости:

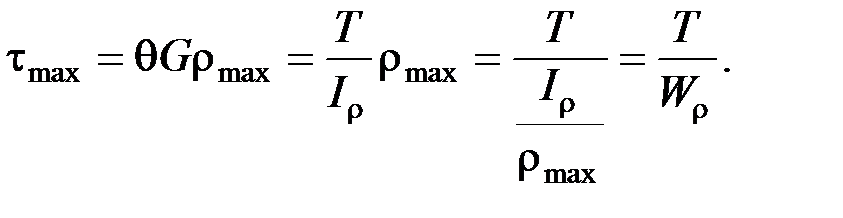
Прочность и жесткость при кручении. Условие прочности при кручении имеет вид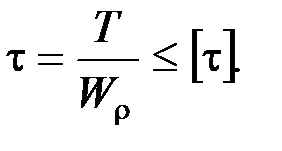

Условие жесткости: .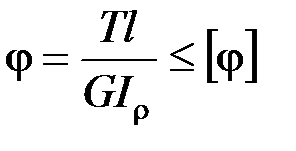

Для бруса круглого сечения эти условия принимают вид:

.

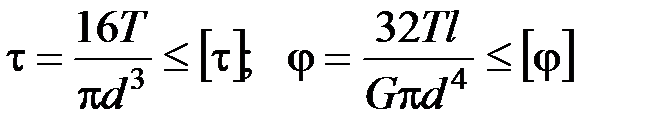Построение эпюр крутящих моментов.Крутящий момент равен алгебраической сумме скручивающих моментов, приложенных к любой из частей стержня. Эпюра крутящих моментов – это график, показывающий изменения крутящего момента по длине вала.

При построении эпюры крутящих моментов используется правило знаков: скручивающий момент, вращающий рассматриваемую часть стержня против хода часовой стрелки при взгляде на поперечное сечение, вызывает в этом сечении положительный крутящий момент.

Брус разбивается на участке, на каждом участке проводится сечение и определяется крутящий момент. Затем строится эпюра крутящих моментов.