Вынужденные колебания. Биения. Затухающие колебания. Добpотность. Пpинцип суперпозиции колебаний

Перейдем теперь к рассмотрению колебаний в системе, на которую действует переменная во времени внешняя сила F(t). Такие колебания называют вынужденными,в отличие от свободныхколебаний, рассмотренных ранее.

Уpавнение вынужденных колебаний имеет вид

тx'' + kx = F(t) (11.1)

где F(t) есть внешняя сила. Уpавнение движения можно переписать в виде

x'' + w²x = F(t)/m (11.2)

где мы снова ввели частоту свободных колебаний ω = k/m.

По математической терминологии, уравнение (11.2) представляет собой неоднородное линейное дифференциальное уравнение с постоянными коэффициентами.Слово "неоднородное" означает, что правая часть этого уравнения отлична от нуля. В математике доказывается теорема, согласно которой общее решение неоднородного линейного дифференциального уравнения с постоянными коэффициентами является суммой двух выражений,

x = x₀+x₁, (11.3)

где x₀ — общее решение однородного уравнения (то есть с правой частью равной нулю), а x₁ — любое частное решение неоднородного уравнения. В данном случае x₀ представляет собой рассмотренные ранее свободные колебания.

Рассмотpим, далее, представляющий особый интерес частный случай, когда вынуждающая сила является простой периодической функцией времени с некоторой частотой γ:

F(t)=fcos(γt + β). (11.4)

Частный интегpал уpавнения (11.2) ищем в виде

x₁ = bcos(γt + β) (11.5)

с тем же периодическим множителем. Подставляя это решение в уравнение

−γ²bcos(γt + β) + ω²bcos(γt + β) = f/m cos(γt + β), (11.6)

мы находим амплитуду вынужденных колебаний

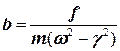(11.7)

Прибавляя решение однородного уравнения, получим общее решение в виде

x = acos(ωt + α)+ 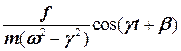(11.8)

Произвольные постоянные a иαопределяются, как и раньше, из начальных условий.

Мы приходим к выводу, что движение под действием периодической вынуждающей силы представляет собой суперпозицию двух колебаний — с собственной частотой системы ω и с частотой вынуждающей силы γ.

Полученное выше решение (11.8) не применимо в случае так называемого резонанса,когда частота вынуждающей силы совпадает с собственной частотой системы, то есть при ω = γ. Второе слагаемое в формуле тx'' + kx = F(t) (11.8) в этом случае обращается в бесконечность. Между тем, очевидно, что за конечное время t система не может приобрести бесконечную энергию под действием конечной силы.

Выясним теперь, как выглядят малые колебания вблизи резонанса, когда γ = ω + ε, где ε — малая величина. Для этого представим общее решение в комплексном виде

х = Ae^iωt + Ве^i(w+ε)t = (А + Be^iεt) e^iωt, (11.9)

где A и B — комплексные постоянные, из которых можно выделить модуль и фазу:

A = ae^iα, B = be^iβ. (11.10)

В силу условия ε < wмы можем рассматривать величину A + Be^iεt в круглых скобках как медленно меняющуюся функцию времени по сравнению с множителем e^iωt. Поэтому движение вблизи резонанса выглядит как малые колебания, но с амплитудой и фазой, медленно меняющимися во времени. Обозначив амплитуду через C, имеем

С =\A + Be^εet\, (11.11)

или, учитывая выражения для A и B, получим

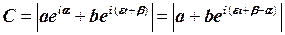(11.12)

Отсюда

C² =a²+ b² + 2abcos(εt + β−α), (11.13)

и мы видим, что амплитуда C колеблется периодически с малой частотой ε между двумя пределами

a−b|≤C≤a + b. (11.14)

Это явление носит название биений(pис. 11.1).