Теорема об изменении кинетической энергии системы
Теорема об изменении кинетической энергии системы в дифференциальной форме: дифференциал от кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему
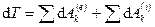 , (207)
, (207)
где кинетическая энергия системы 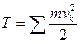 , элементарная работа внешних и внутренних сил соответственно
, элементарная работа внешних и внутренних сил соответственно 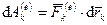 и
и 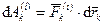 .
.
Если обе части (207) проинтегрировать между двумя положениями системы – начальным и конечным, в которых соответственно кинетическая энергия 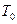 и
и 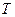 , то, изменяя порядок суммирования и интегрирования, имеем
, то, изменяя порядок суммирования и интегрирования, имеем
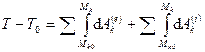 ,
,
или
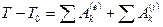 , (208)
, (208)
где 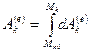 – работа внешней силы для точки
– работа внешней силы для точки 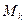 системы при ее перемещении из начального положения
системы при ее перемещении из начального положения 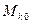 в конечное положение
в конечное положение 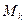 ,
, 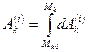 соответственно работа внутренней силы, действующей на точку
соответственно работа внутренней силы, действующей на точку 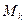 .
.
Формула (208) выражает теорему об изменении кинетической энергии системы в конечной или интегральной форме: изменение кинетической энергии системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних сил, действующих на систему, на соответствующих перемещениях точек системы при том же перемещении системы.
Частный случай. Для абсолютно твердого тела сумма работ всех внутренних сил системы равна нулю:
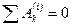 .
.
Т.о., теорему об изменении кинетической энергии, например, в конечной форме можно представить в виде
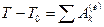 , (209)
, (209)
Изменение кинетической энергии твердого тела при каком-либо перемещении равно сумме работ всех внешних сил, действующих ни тело, на соответствующих перемещениях точек тела при том же перемещении твердого тела.
В отличие от рассмотренных других общих теорем динамики системы в теорему об изменении кинетической энергии могут входить внутренние силы.
Принцип Даламбера
Дата добавления: 2017-09-01; просмотров: 1427;











