Силы инерции твердого тела в частных случаях его движения
При поступательном движении. Если твердое тело движется поступательно, то ускорения его точек одинаковы. Силы инерции этих точек составляют систему параллельных сил, направленных в одну сторону. Такая система сил приводится к равнодействующей силе 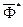 , которая равна главному вектору, т. е.
, которая равна главному вектору, т. е.
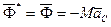 .
.
Линия действия равнодействующей силы инерции в этом случае проходит через центр масс, так как главный момент сил инерции точек тела относительно центра масс
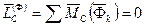 .
.
Действительно, согласно следствию из принципа Даламбера (12) для центра масс, имеем
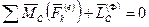 .
.
При поступательном движении тело не совершает вращения вокруг центра масс и поэтому 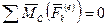 . Следовательно,
. Следовательно, 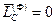
При вращении вокруг неподвижной оси. Если выбрать за центр приведения сил инерции точку 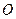 на оси вращения
на оси вращения 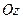 , то в этой точке получим главный вектор и главный момент сил инерции:
, то в этой точке получим главный вектор и главный момент сил инерции:
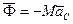 ,
, 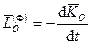 .
.
Если центр масс находится на оси вращения, то 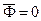 . Проекции главного момента сил инерции на неподвижные оси координат в общем случае можно вычислить по формулам
. Проекции главного момента сил инерции на неподвижные оси координат в общем случае можно вычислить по формулам
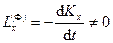 ,
, 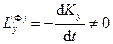 ,
, 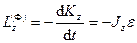 .
.
(Моменты сил инерции 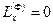 и
и 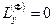 , если ось
, если ось 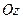 является главной осью инерции для точки
является главной осью инерции для точки 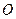 .)
.)
При плоском движении. Выбрав за центр приведения сил инерции центр масс, получим в этой точке главный вектор и главный момент сил инерции. Для главного вектора сил инерции имеем
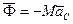 .
.
Для данного момента сил инерции относительно центра масс 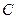 , который является движущейся точкой при плоском движении тела, получим формулы, аналогичные формуле (149), выведенной для неподвижной точки
, который является движущейся точкой при плоском движении тела, получим формулы, аналогичные формуле (149), выведенной для неподвижной точки 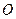 .
.
Согласно следствию из принципа Даламбера (147), главный момент сил инерции относительно центра масс удовлетворяет условию
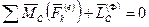 .
.
С другой стороны, из теорем об изменении кинетического момента относительно центра масс для абсолютного и относительного движений имеем
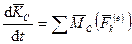 ,
, 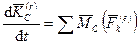 .
.
Из этих соотношений следует
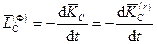 .
.
Проекции главного момента на оси координат с началом в центре масс и движущиеся поступательно вместе с центром масс соответственно
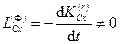 ,
, 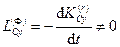 ,
, 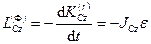 ,
,
где ось 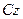 перпендикулярна плоскости, параллельно которой совершают движение точки тела.
перпендикулярна плоскости, параллельно которой совершают движение точки тела.
Моменты сил инерции 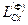 и
и 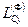 вычисляются так же, как и при вращении тела вокруг неподвижной оси. Они равны пулю, если ось
вычисляются так же, как и при вращении тела вокруг неподвижной оси. Они равны пулю, если ось 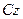 является главной осью инерции для точки
является главной осью инерции для точки 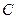 . Это, в частности выполняется, если тело имеет плоскость симметрии, проходящую через центр масс и параллельную плоскости движения тела.
. Это, в частности выполняется, если тело имеет плоскость симметрии, проходящую через центр масс и параллельную плоскости движения тела.
ЛЕКЦИЯ № 9
Дата добавления: 2017-09-01; просмотров: 1676;











