Принцип Даламбера для материальной точки
Принцип Даламбера для свободной материальной точки эквивалентен основному закону динамики. Для несвободной точки он эквивалентен основному закону вместе с аксиомой связей.
Уравнение движения материальной точки массой относительно инерциальной системы отсчета под действием приложенных активных сил и реакций связей имеет вид
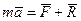 . (210)
. (210)
Сила 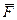 является равнодействующей активных сил,
является равнодействующей активных сил, 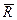 – равнодействующей реакций связей,
– равнодействующей реакций связей, 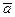 – ускорением точки относительно инерциальной системы отсчета. Назовем силой инерции материальной точки произведение массы точки на вектор ускорения, взятое с обратным знаком, т.е.
– ускорением точки относительно инерциальной системы отсчета. Назовем силой инерции материальной точки произведение массы точки на вектор ускорения, взятое с обратным знаком, т.е. 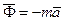 Если использовать понятие силы инерции точки и перенести все слагаемые (209) в правую часть уравнения, то получим
Если использовать понятие силы инерции точки и перенести все слагаемые (209) в правую часть уравнения, то получим
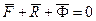 . (210)
. (210)
Так как силы 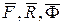 образуют систему сходящихся сил и удовлетворяют условию (37), то они являются системой сил, эквивалентной нулю, т.е.
образуют систему сходящихся сил и удовлетворяют условию (37), то они являются системой сил, эквивалентной нулю, т.е.
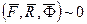 . (211)
. (211)
Уравнение (210) или эквивалентное ему условие (211) выражает принцип Даламбера для точки: при движении материальной точки активные силы и реакции связей вместе с силой инерции точки образуют равновесную систему сил.
Из (210) в проекциях на координатные оси получаем три условия равновесия сил:
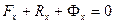 ,
, 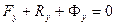 ,
, 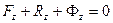 . (212)
. (212)
Ускорение точки относительно инерциальной системы отсчета можно разложить на составляющие по осям декартовой системы координат, а также на касательное и нормальное ускорения и на переносное, относительное ускорения и ускорение Кориолиса, если движение точки считать сложным, состоящим из переносного и относительного. Соответственно силу инерции 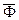 можно разложить на такие же составляющие:
можно разложить на такие же составляющие:
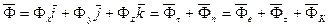 . (213)
. (213)
Касательная сила инерции 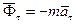 , где
, где 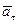 – касательное ускорение; нормальная, или центробежная, сила инерции
– касательное ускорение; нормальная, или центробежная, сила инерции 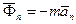 , где
, где 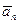 – нормальное ускорение. Переносная и относительная силы инерции, а также сила инерции Кориолиса через ускорения выражаются соответственно так:
– нормальное ускорение. Переносная и относительная силы инерции, а также сила инерции Кориолиса через ускорения выражаются соответственно так: 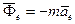 ,
, 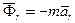 ,
, 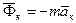 .
.
Аналогично выражаются через проекции ускорения на прямоугольные оси координат проекции силы инерции 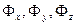 .
.
Дата добавления: 2017-09-01; просмотров: 1360;











