Плоское (плоскопараллельное) движение твердого тела
Плоским движением твердого тела называют такое его движение, при котором каждая его точка все время движется в одной и той же плоскости. Плоскости, в которых движутся отдельные точки, параллельны между собой и параллельны одной и той же неподвижной плоскости. Поэтому плоское движение твердого тела часто называют плоскопараллельным движением. Траектории точек тела при плоском движении являются плоскими кривыми.

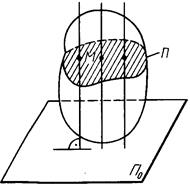 Пусть твердое тело совершает плоское движение, параллельное неподвижной плоскости
Пусть твердое тело совершает плоское движение, параллельное неподвижной плоскости 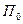 (рис. 35). Тогда любая прямая, перпендикулярная этой плоскости и жестко скрепленная своими точками с движущимся телом, будет двигаться поступательно, т. е. все точки этой прямой движутся одинаково.
(рис. 35). Тогда любая прямая, перпендикулярная этой плоскости и жестко скрепленная своими точками с движущимся телом, будет двигаться поступательно, т. е. все точки этой прямой движутся одинаково.
Значит, для изучения движения точек, лежащих на рассматриваемой прямой, достаточно изучить движение одной точки этой прямой, например точки 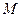 . Рассуждая аналогично для любой другой прямой, перпендикулярной плоскости
. Рассуждая аналогично для любой другой прямой, перпендикулярной плоскости 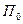 и скрепленной с движущимся твердым телом, можно сделать вывод, что для изучения плоского движения твердого тела достаточно изучить движение точек этого тела, лежащих в какой-либо плоскости
и скрепленной с движущимся твердым телом, можно сделать вывод, что для изучения плоского движения твердого тела достаточно изучить движение точек этого тела, лежащих в какой-либо плоскости 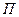 , параллельной неподвижной плоскости
, параллельной неподвижной плоскости 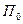 , т.е. точек тела, лежащих в сечении рассматриваемого тела плоскостью
, т.е. точек тела, лежащих в сечении рассматриваемого тела плоскостью 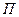 и образующих плоскую фигуру.
и образующих плоскую фигуру.
Таким образом, для изучения плоского движения твердого тела достаточно изучить движение плоской фигуры в ее плоскости, параллельной неподвижной плоскости 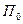 . Положение фигуры на ее плоскости полностью определяется положением отрезка прямой линии, жестко скрепленной с этой плоской фигурой. Различные по форме твердые тела, совершающие плоское движение, имеют в сечениях разные плоские фигуры. В общем случае за плоскую фигуру примем всю плоскость и, следовательно, рассмотрим движение этой подвижной плоскости по другой, неподвижной плоскости.
. Положение фигуры на ее плоскости полностью определяется положением отрезка прямой линии, жестко скрепленной с этой плоской фигурой. Различные по форме твердые тела, совершающие плоское движение, имеют в сечениях разные плоские фигуры. В общем случае за плоскую фигуру примем всю плоскость и, следовательно, рассмотрим движение этой подвижной плоскости по другой, неподвижной плоскости.
Для характеристики вращательной части плоского движения твердого тела вокруг подвижной оси, проходящей через выбранный полюс, аналогично случаю вращения твердого тела вокруг неподвижной оси можно ввести понятия угловой скорости 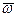 и углового ускорения
и углового ускорения 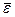 . Если угол поворота вокруг подвижной оси, проходящей через полюс, обозначить
. Если угол поворота вокруг подвижной оси, проходящей через полюс, обозначить 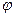 , то
, то
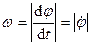 ,
, 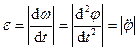 .
.
Так как вращательная часть движения не зависит от выбора полюса, то и характеристики этой части движения – угловая скорость и угловое ускорение – также не зависят от выбора полюса.
При плоском движении тела угловую скорость и угловое ускорение можно считать векторами, направленными по подвижной оси, перпендикулярной плоскости фигуры и проходящей через выбранный полюс. Вектор угловой скорости 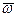 при плоском движении фигуры направлен по подвижной оси так, чтобы с конца его стрелки можно было видеть вращение фигуры против часовой стрелки. Вектор углового ускорения
при плоском движении фигуры направлен по подвижной оси так, чтобы с конца его стрелки можно было видеть вращение фигуры против часовой стрелки. Вектор углового ускорения 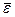 при ускоренном вращении фигуры совпадает с направлением вектора угловой скорости
при ускоренном вращении фигуры совпадает с направлением вектора угловой скорости 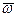 , а при замедленном вращении эти векторы имеют противоположные направления. Вектор углового ускорения является первой производной по времени от вектора угловой скорости, т. е.
, а при замедленном вращении эти векторы имеют противоположные направления. Вектор углового ускорения является первой производной по времени от вектора угловой скорости, т. е. 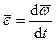 .
.
Дата добавления: 2017-09-01; просмотров: 1256;











