Ускорение Кориолиса
Рассмотрим ускорение Кориолиса и его свойства. Оно определяется формулой (81)
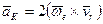 .
.
Угловую скорость вращательной части движения подвижной системы отсчета, т.е. угловую скорость переносного движения, обозначили как 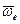 .
.
Ускорение Кориолиса является результатом взаимного влияния двух движений: переносного и относительного. Часть его 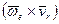 получается вследствие изменения переносной скорости точки из-за относительного движения. Другая его часть, тоже
получается вследствие изменения переносной скорости точки из-за относительного движения. Другая его часть, тоже 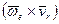 , есть результат изменения относительной скорости вследствие переносного движения.
, есть результат изменения относительной скорости вследствие переносного движения.
Модуль ускорения Кориолиса в соответствии с (81) определяется выражением
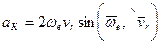 . (84)
. (84)
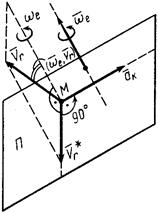
Для определения ускорения Кориолиса очень удобно правило Жуковского Н. Е. Оно основано на формуле (81). Пусть имеем точку 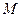 , движущуюся с относительной скоростью
, движущуюся с относительной скоростью 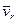 , (рис. 34). Построим плоскость
, (рис. 34). Построим плоскость 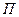 , перпендикулярную угловой скорости переносного вращения
, перпендикулярную угловой скорости переносного вращения 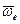 , и спроецируем
, и спроецируем 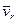 на эту плоскость. Проекцию обозначим
на эту плоскость. Проекцию обозначим 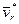 . Она является вектором; ее модуль
. Она является вектором; ее модуль
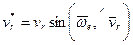 .
.
 Ускорение Кориолиса выразится в форме
Ускорение Кориолиса выразится в форме
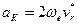 . (84')
. (84')
Учитывая (81) и (84'), получаем правило Жуковского: модуль ускорения Кориолиса равен удвоенному произведению угловой скорости переносного вращения на модуль проекции относительной скорости на плоскость, перпендикулярную оси переносного вращения; чтобы получить направление ускорения Кориолиса, следует вектор проекции относительной скорости 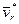 повернуть на 90° вокруг оси, параллельной оси переносного вращения, в направлении этого вращения.
повернуть на 90° вокруг оси, параллельной оси переносного вращения, в направлении этого вращения.
Рассмотрим случаи обращения в нуль ускорения Кориолиса. Из (84) следует, что 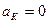 , если:
, если:
1) 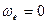 , т.е. переносное движение является поступательным;
, т.е. переносное движение является поступательным;
2) 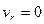 , т.е. в те моменты времени, в которые происходит изменение направления относительного движения;
, т.е. в те моменты времени, в которые происходит изменение направления относительного движения;
3) 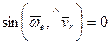 , т.е. когда скорость относительного движения
, т.е. когда скорость относительного движения 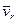 параллельна угловой скорости переносного вращения
параллельна угловой скорости переносного вращения 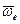 .
.
ЛЕКЦИЯ № 5
Дата добавления: 2017-09-01; просмотров: 2114;











