Ускорения точек плоской фигуры
Рассматривая плоское движение плоской фигуры как сложное, состоящее из переносного поступательного вместе с полюсом 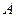 и относительного вращательного вокруг
и относительного вращательного вокруг 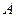 , по теореме о сложении ускорений для точки
, по теореме о сложении ускорений для точки 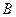 имеем
имеем
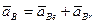 . (92)
. (92)
Так как переносное движение является поступательным вместе с точкой 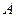 фигуры, то переносное ускорение
фигуры, то переносное ускорение
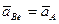
Относительное ускорение 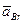 точки
точки 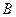 от вращения вокруг полюса
от вращения вокруг полюса 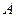 обозначим
обозначим 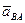 . После этого формула (92) принимает вид
. После этого формула (92) принимает вид
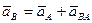 . (93)
. (93)
т. е. ускорение какой-либо точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки от вращательного движения плоской фигуры вокруг полюса.
Ускорение от относительного вращательного движения вокруг полюса, как и в случае вращения тела вокруг неподвижной оси, состоит из касательной и нормальной составляющих 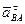 и
и 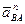 :
:
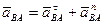 , (94)
, (94)
причем
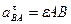 , (95)
, (95)
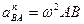 , (96)
, (96)
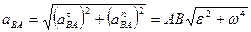 . (97)
. (97)
Касательное относительное ускорение 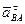 направлено по перпендикуляру к отрезку
направлено по перпендикуляру к отрезку 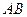 в сторону дуговой стрелки углового ускорения
в сторону дуговой стрелки углового ускорения 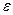 (рис. 38,а). Нормальное относительное ускорение
(рис. 38,а). Нормальное относительное ускорение 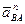 соответственно направлено по линии
соответственно направлено по линии 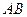 от точки
от точки 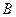 к полюсу
к полюсу 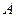 . Наконец, полное относительное ускорение
. Наконец, полное относительное ускорение 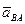 составляет с отрезком
составляет с отрезком 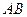 угол
угол 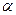 , тангенс которого можно определить по формуле
, тангенс которого можно определить по формуле
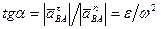 . (98)
. (98)
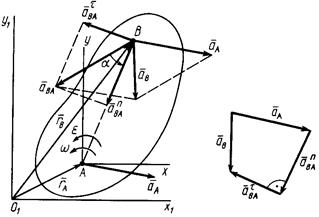
а) б)
Рис. 38
Из формулы (98) следует, что угол 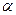 для всех точек плоской фигуры одинаков. При
для всех точек плоской фигуры одинаков. При 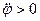 угол
угол 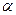 от ускорения
от ускорения 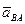 к отрезку
к отрезку 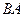 надо откладывать против часовой стрелки. При
надо откладывать против часовой стрелки. При 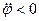 его надо откладывать по часовой стрелке, т. е. во всех случаях, независимо от направления вращения фигуры, угол
его надо откладывать по часовой стрелке, т. е. во всех случаях, независимо от направления вращения фигуры, угол 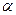 всегда надо откладывать в направлении дуговой стрелки углового ускорения. В соответствии с (93) и (94) можно построить в выбранном масштабе многоугольник ускорений для точки
всегда надо откладывать в направлении дуговой стрелки углового ускорения. В соответствии с (93) и (94) можно построить в выбранном масштабе многоугольник ускорений для точки  (рис. 38,б).
(рис. 38,б).
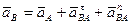 .
.
Дата добавления: 2017-09-01; просмотров: 1118;











