Понятие о центре изгиба тонкостенных стержней.
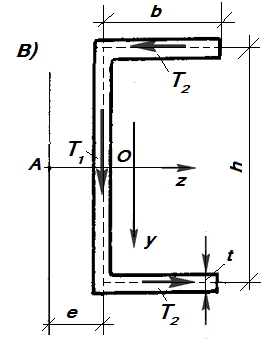
Как было отмечено выше, касательные напряжения в поперечных сечениях тонкостенных стержней образуют поток, параллельный контурным линиям каждого элемента стержня. В некоторых случаях этот поток может создавать момент относительно оси стержня. Рассмотрим изгиб консольного стержня швеллерного сечения в плоскости 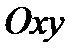 (рис.17.7,а). Характер распределении касательных напряжений такой же, как и в двутавре . В стенке действуют напряжения
(рис.17.7,а). Характер распределении касательных напряжений такой же, как и в двутавре . В стенке действуют напряжения 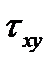 , а в полках - касательные напряжения
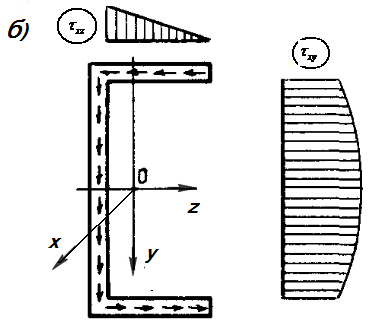
, а в полках - касательные напряжения 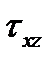 .Эпюры этих напряжений приведены на рис.17.7,б.
.Эпюры этих напряжений приведены на рис.17.7,б.

| 
| 
|
Рис.17.7 Касательные напряжения в тонкостенном стержне 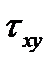 ,
, 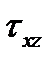
Равнодействующей касательных напряжений в стенке является сила 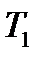 , которая практически равна поперечной силе
, которая практически равна поперечной силе 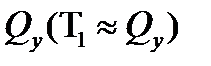 . Касательные напряжения в полках приводятся к равнодействующим силам
. Касательные напряжения в полках приводятся к равнодействующим силам 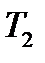 (рис. 17.7,в). Нетрудно видеть, что равнодействующие касательных сил
(рис. 17.7,в). Нетрудно видеть, что равнодействующие касательных сил 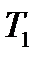 ,
, 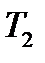 дают момент относительно центра тяжести сечения, вызывающий закручивание стержня. Таким образом, если линия действия силы
дают момент относительно центра тяжести сечения, вызывающий закручивание стержня. Таким образом, если линия действия силы 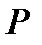 проходит через центр тяжести сечения
проходит через центр тяжести сечения  , то балка будет испытывать изгиб с кручением, что является нежелательным.
, то балка будет испытывать изгиб с кручением, что является нежелательным.
Определим положение точки плоскости, при прохождении через которую линии действия силы 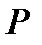 поток касательных напряжений не будет вызывать закручивание стержня. Очевидно, что такая точка
поток касательных напряжений не будет вызывать закручивание стержня. Очевидно, что такая точка 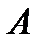 расположена на оси
расположена на оси 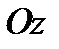 левее стенки швеллера (рис.17.7,в), поскольку при этом равнодействующие касательных сил
левее стенки швеллера (рис.17.7,в), поскольку при этом равнодействующие касательных сил 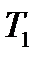 и
и 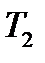 будут давать моменты разных знаков относительно точки
будут давать моменты разных знаков относительно точки 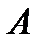 . Составим уравнение равновесия
. Составим уравнение равновесия
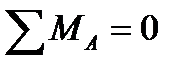 ,
, 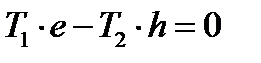 . Отсюда находим координату точки
. Отсюда находим координату точки 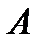
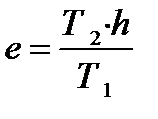 , , 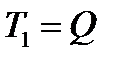
| (17.18) |
Таким образом, если линия действия силы будет проходить через точку 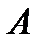 , то стержень будет испытывать только изгиб. Поэтому точка
, то стержень будет испытывать только изгиб. Поэтому точка 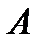 называется центром изгиба. В общем случае центр изгиба не совпадает с центром тяжести сечения и его положение подлежит определению.
называется центром изгиба. В общем случае центр изгиба не совпадает с центром тяжести сечения и его положение подлежит определению.
Для швеллера имеем: касательные напряжения в полке 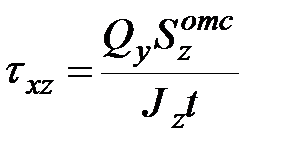 ; статический момент полки
; статический момент полки 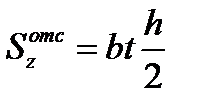 . Эпюра
. Эпюра 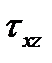 имеет вид треугольника с наибольшей ординатой, равной
имеет вид треугольника с наибольшей ординатой, равной 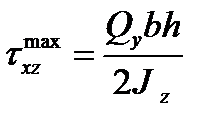 . Равнодействующие в верхней и нижней полках одинаковы и равны
. Равнодействующие в верхней и нижней полках одинаковы и равны 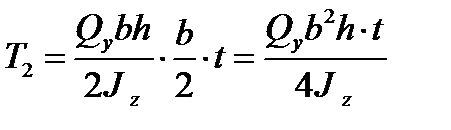 . Подставляем
. Подставляем 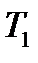 ,
, 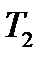 в формулу (17.18) (
в формулу (17.18) ( 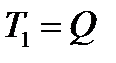 ), получаем
), получаем
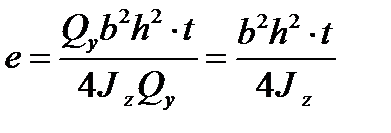
| (17.19) |
Центр изгиба это точка, через которую проходят равнодействующая внутренних касательных сил 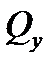 и плоскость действия внешних сил, при этом изгиб не сопровождается кручением.
и плоскость действия внешних сил, при этом изгиб не сопровождается кручением.
На рис 17.8 показаны 4-различных сечения с указанием положения центра изгиба (т. 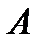 )
)
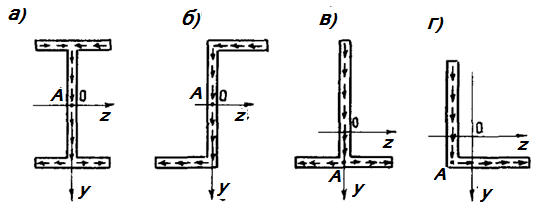
Рис.17.8 Центр изгиба тонкостенных сечений
Дата добавления: 2017-09-01; просмотров: 3604;











