Свободное кручение стержней некруглого сечения
При рассмотрении деформации кручения стержней круглого сечения мы пользовались гипотезой плоских сечений. Однакооказалось, что круглое сечение – это редкое, хотя и важное, исключение когда сечения при закручивании не искривляясь поворачиваются как плоские диски вокруг оси 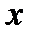 .
.
При кручении стержней некруглого поперечного сечения гипотеза плоских сечений не выполняется. Происходит так называемая депланация сечений - сечения искривляются (рис.17.6)
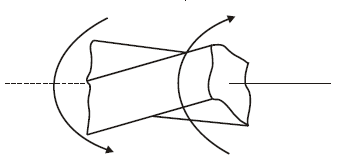
Рис.17.6 Депланация прямоугольного сечения при кручении
Точное решение задачи кручения для некоторых типов поперечных сечений дается в курсе теории упругости.
Для удобства использования результаты расчета стержней любого поперечного сечения принято представлять в той же форме, что и для стержней круглого поперечного сечения, а именно:
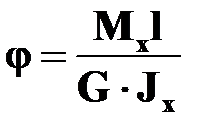 ;
; 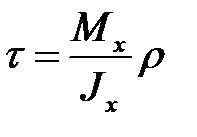 ;
; 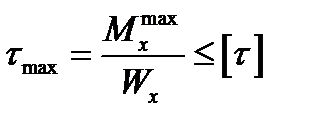 ;
; 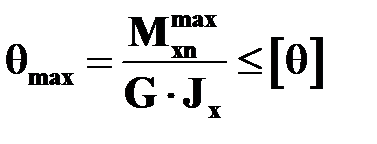 .
.
Здесь 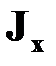 ,
, 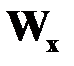 - эмпирические или расчетные коэффициенты, называемые соответственно полярный момент инерции и момент сопротивления при кручении.
- эмпирические или расчетные коэффициенты, называемые соответственно полярный момент инерции и момент сопротивления при кручении.
Для стержней некруглого поперечного сечения 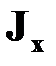 ,
, 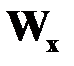 берутся из справочника.
берутся из справочника.
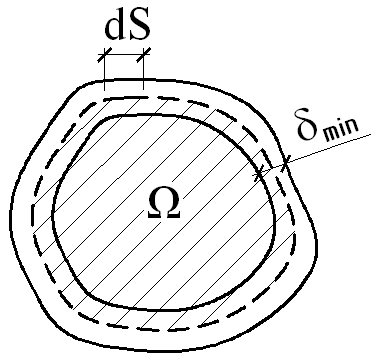
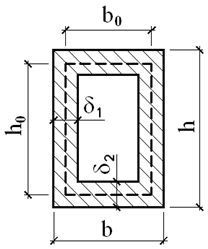
Формулы для вычисления наибольших касательных напряжении 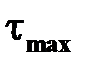 и положение точек, вблизи которых они имеют место, для некоторых сечений при кручении приведены в табл.17.1. В таблице 17.1 представлены также геометрические характеристики сечений тонкостенные стержней открытого и замкнутого профилей. Стержень называется тонкостенным, если толщина стенки
и положение точек, вблизи которых они имеют место, для некоторых сечений при кручении приведены в табл.17.1. В таблице 17.1 представлены также геометрические характеристики сечений тонкостенные стержней открытого и замкнутого профилей. Стержень называется тонкостенным, если толщина стенки 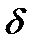 значительно меньше размеров поперечного сечения. Срединная линия (на рисунках показана пунктиром) это линия равноудаленная от боковых поверхностей стержня.
значительно меньше размеров поперечного сечения. Срединная линия (на рисунках показана пунктиром) это линия равноудаленная от боковых поверхностей стержня.
Таблица 17.1
Геометрические характеристики сечений стержней, испытывающих кручение, и формулы для определения наибольших касательных напряжений.
| Поперечное сечение стержня | Момент сопротивления кручению 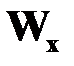
| Момент инерции при кручении 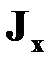
| Положение точек, где действуют наибольшие касательные напряжения, величина 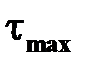
|
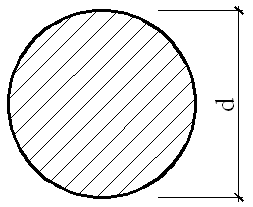
|
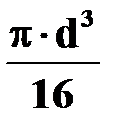
|
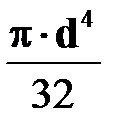
| Во всех точках по контуру круга
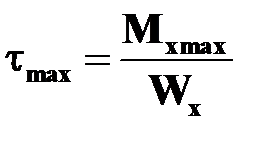
|
|
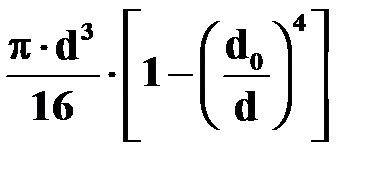
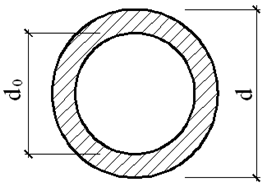
|
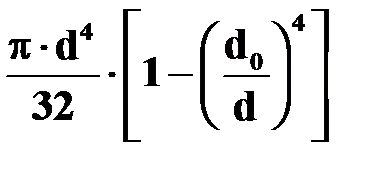
| Во всех точках наружного контура
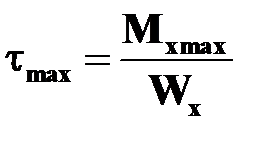 .
В точках внутреннего контура .
В точках внутреннего контура
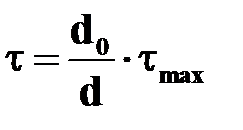
|
|
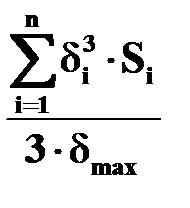
|
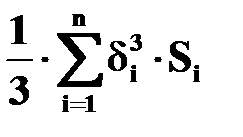
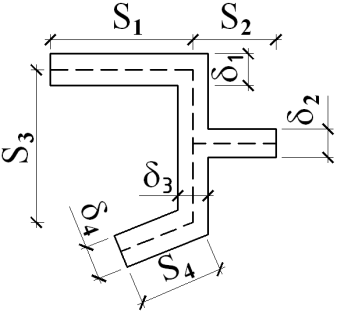
| В точках контура посредине стороны с наибольшей толщиной стенки
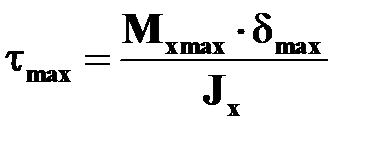 .
В середине .
В середине 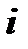 -го участка -го участка 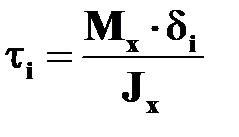
|
| 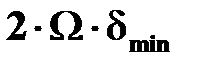
 -площадь сечения, ограниченная срединной линией контура -площадь сечения, ограниченная срединной линией контура
| 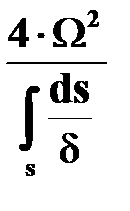 ,
при ,
при 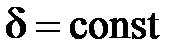 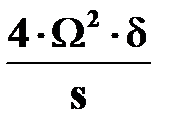 ;
s-длина срединной линии ;
s-длина срединной линии
| На участке с наименьшей толщиной стенки
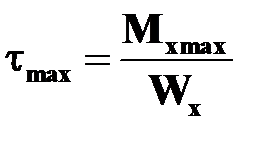 . .
|
|
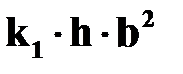
|
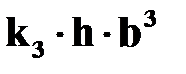
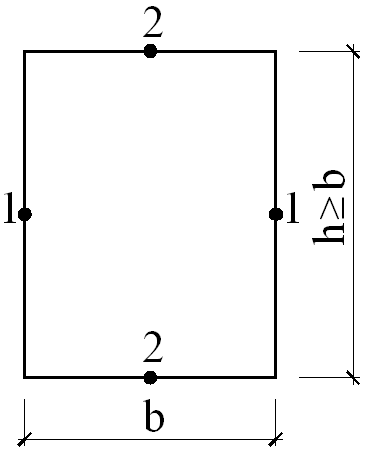
| В середине длинных сторон контура (точки 1)
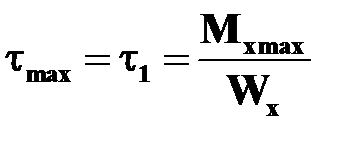 .
В середине коротких сторон контура (точки 2) .
В середине коротких сторон контура (точки 2)
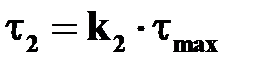
|
|
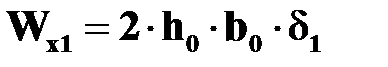
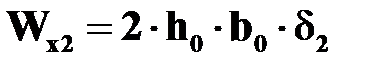
|
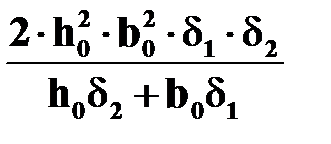
| Посредине длинной стороны
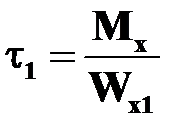 .
Посредине короткой стороны .
Посредине короткой стороны
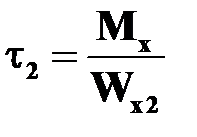
|
Коэффициенты 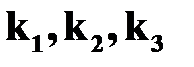 для расчета прямоугольных сечений на кручение представлены в табл.17.2
для расчета прямоугольных сечений на кручение представлены в табл.17.2
Таблица 17.2

Дата добавления: 2017-09-01; просмотров: 1943;











