Кручение стержней с круглым поперечным сечением
17.1 Расчеты на прочность.
Обеспечение прочности при кручении элементов строительных конструкций круглого сечения производится по методу допускаемых напряжений на основе неравенства
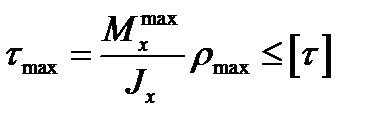 , ,
| (17.1) |
где 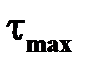 – наибольшее и
– наибольшее и 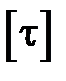 - допускаемое касательные напряжения в поперечном сечении стержня;
- допускаемое касательные напряжения в поперечном сечении стержня; 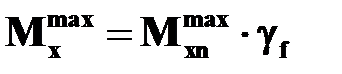 - наибольший по абсолютной величине крутящий момент, определяемый от расчетных нагрузок,
- наибольший по абсолютной величине крутящий момент, определяемый от расчетных нагрузок, 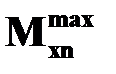 – наибольший по абсолютной величине крутящий момент от нормативных нагрузок;
– наибольший по абсолютной величине крутящий момент от нормативных нагрузок; 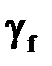 – коэффициент надежности по нагрузке.
– коэффициент надежности по нагрузке.
Левую часть неравенства перепишем в виде:
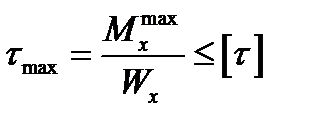 , , 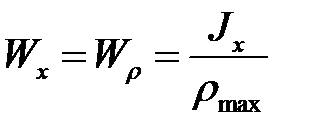 . .
| (17.2) |
Здесь - 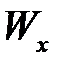 , (
, ( 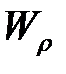 ) -момент сопротивления поперечного сечения стержня при кручении (полярный момент сопротивления).
) -момент сопротивления поперечного сечения стержня при кручении (полярный момент сопротивления).
Для круглого сечения 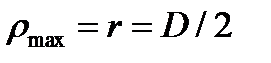
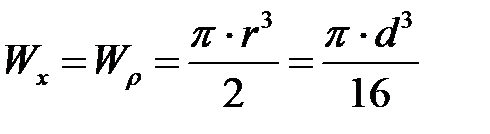 . .
| (17.3) |
Для полого толстостенного цилиндра
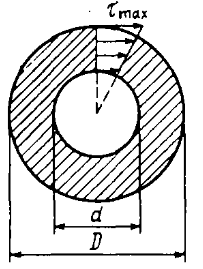
| 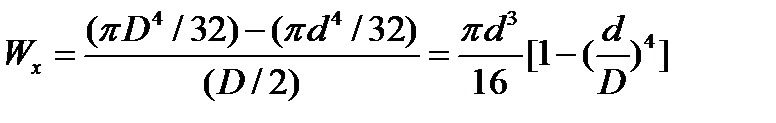 . .
| (17.4) |
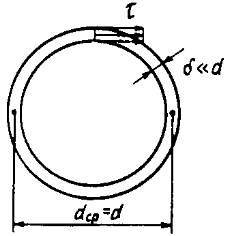
Для тонкостенного кольцевого сечения, когда толщина стенки 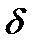 во много раз меньше среднего диаметра сечения
во много раз меньше среднего диаметра сечения 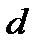 , можно считать, что касательные напряжения
, можно считать, что касательные напряжения 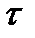 равномерно распределены по толщине
равномерно распределены по толщине 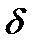 и равны средним напряжениям.
и равны средним напряжениям.
|
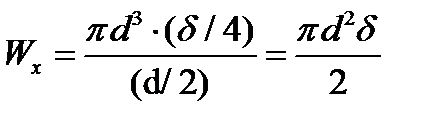 . .
| ( 17.5) |
Допускаемое касательное напряжение 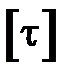 зависит от применяемой гипотезы (теории) прочности
зависит от применяемой гипотезы (теории) прочности
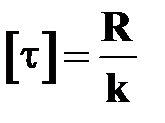 , ,
| (17.6) |
где: 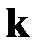 равно 1, 1+n, 2,
равно 1, 1+n, 2, 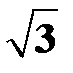 соответственно при использовании 1-й, 2-й, 3-й и 4-й гипотез прочности;
соответственно при использовании 1-й, 2-й, 3-й и 4-й гипотез прочности;
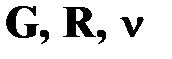 – модуль упругости при кручении (модуль сдвига), расчетное сопротивление и коэффициент Пуассона материала;
– модуль упругости при кручении (модуль сдвига), расчетное сопротивление и коэффициент Пуассона материала;
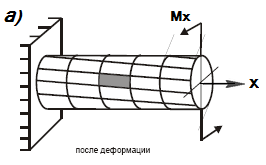
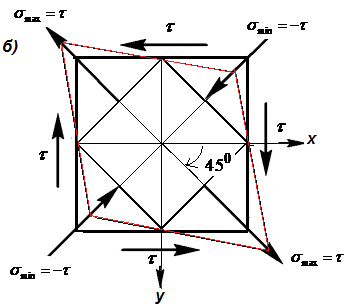
Действительно, при кручении стержня, элемент, выделенный в окрестности точки, испытывает сложное напряженное состояние - чистый сдвиг (рис.17.1а,б)
| 
|
Рис. 17.1 Деформация элемента стержня при кручении
Чистый сдвиг – частный случай плоского напряженного состояния: 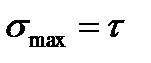 ,
, 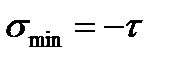 . При переходе к пространственному напряженному состоянию главные напряжения принимают значения:
. При переходе к пространственному напряженному состоянию главные напряжения принимают значения: 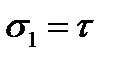 ,
, 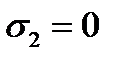 ,
, 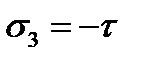 .
.
По первой теории прочности эквивалентное напряжение (приведенное напряжение) определится по формуле 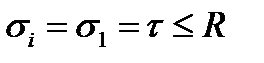 и условие прочности примет вид:
и условие прочности примет вид: 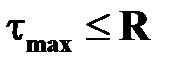 .
.
По второй теории прочности 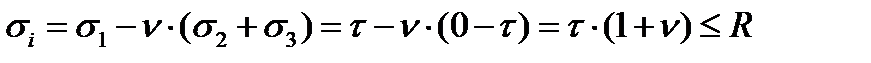 и условие прочности примет вид:
и условие прочности примет вид: 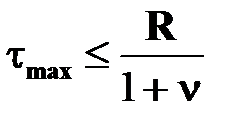 .
.
По третьей теории прочности 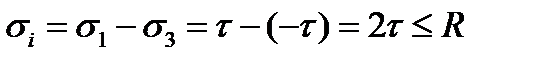 и условие прочности примет вид:
и условие прочности примет вид: 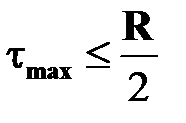 .
.
По четвертой теории прочности 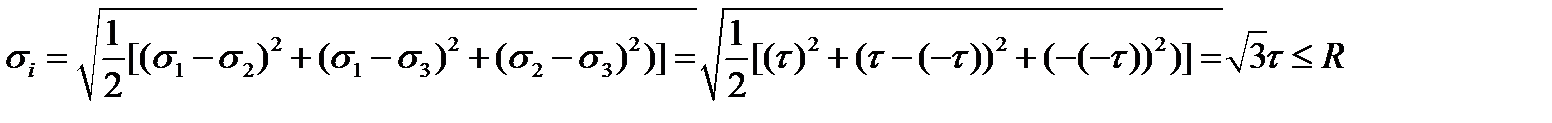 и условие прочности примет вид:
и условие прочности примет вид: 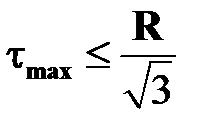 .
.
Дата добавления: 2017-09-01; просмотров: 1342;











