Кручение в упругопластической стадии

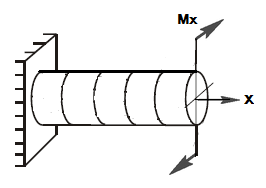
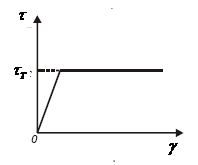
До сих пор предполагалось, что материал скручиваемого стержня деформируется линейно - упруго в соответствии с законом Гука. Заменим реальную криволинейную диаграмму сдвига условной – диаграммой Прандтля при сдвиге (рис.17.3)

Рис.17.3 Диаграмма Прандтля при сдвиге

Будем считать, что при 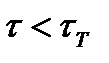(предел текучести при сдвиге) справедлив закон Гука и материал деформируется линейно-упруго. При напряжениях 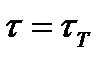возникают пластические деформации сдвига, значения которых неограниченны, а напряжения остаются постоянными и равными .

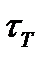С использованием указанного упрощения выясним, как будет видоизменяться эпюра касательных напряжений в сечении при постепенном возрастании крутящего момента 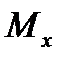. В упругой стадии напряжения 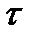распределены вдоль диаметра по линейному закону. При возрастании момента 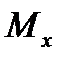пропорционально возрастают и все напряжения. Окончание этой стадии определяет равенство

,

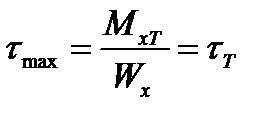(17.10)

когда в точках на контуре сечения впервые появится текучесть (рис.17.4а).

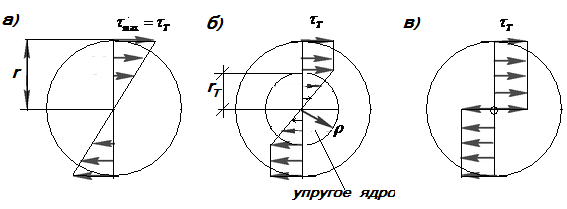
Рис.17.4 Образование пластического шарнира при кручении

Соответствующий крутящий момент обозначим 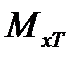. Из равенства(17.10) получим

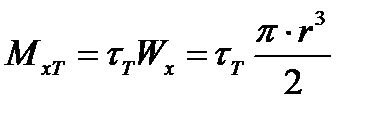
(17.11)

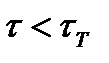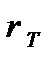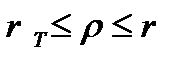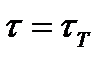При дальнейшем возрастании момента пластическая зона будет все больше проникать в глубь вала (рис.17.4,б), а сечение разделится на две зоны: упругое ядро, где с радиусом и пластическую кольцевую зону ,где . Соответствующий крутящий момент представим как сумму

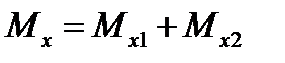
(17.12)

, где момент упругого ядра найден из (17.11) при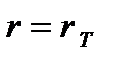

,

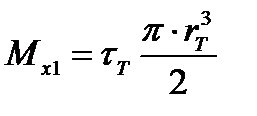(17.13)

а момент пластической кольцевой зоны

.

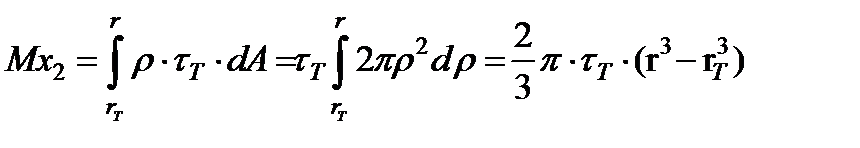(17.14)

Момент упругого ядра 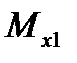связан с его погонным углом закручивания соотношением (см.16.7)

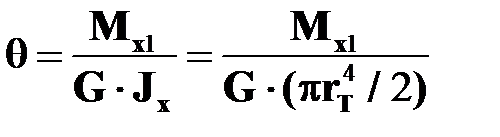
(17.15)

Это выражение является общим для упругого ядра и пластической зоны вследствие того, что в упругопластической стадии, как и в упругой, по-прежнему справедлива гипотеза плоских сечений.

Из (17.13) подставляем 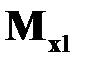в (17.15), получаем 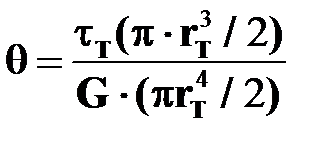.Сокращаем на 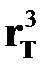и находим радиус

.

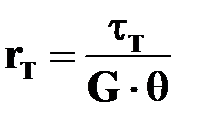(17.16)

После подстановки (17.16) в выражения (17.13) и (17.14) суммарный крутящий момент примет вид

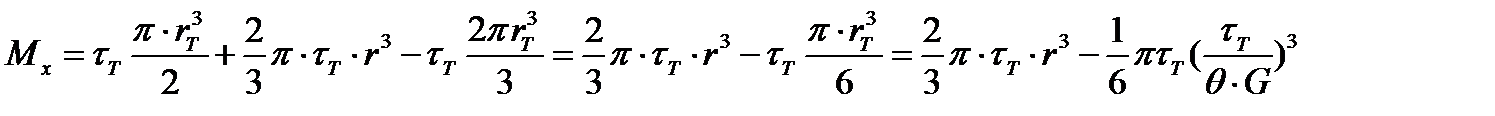, или

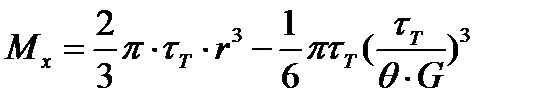
(17.17)

График зависимости (17.17) от 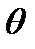изображен на рис.17.5

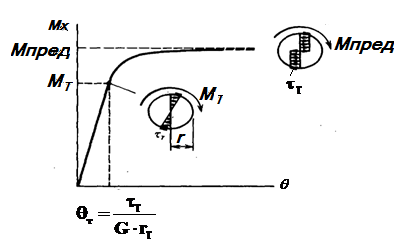
Рис. 17.5 Зависимость между относительным углом закручивания

и крутящим моментом в упругопластической стадии

При 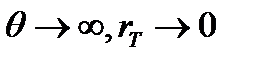пластическая зона стремится охватить все сечение и внутренний момент стремится к своему предельному значению: .

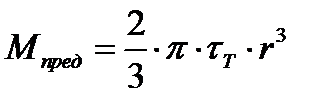Состояние стержня, когда во всех точках его поперечного сечения возникают пластические деформации, называют пластическим шарниром. Стержень превращается как бы в пластический механизм, в котором углы закручивания неограниченно растут при постоянном моменте .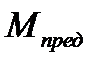

Соотношение 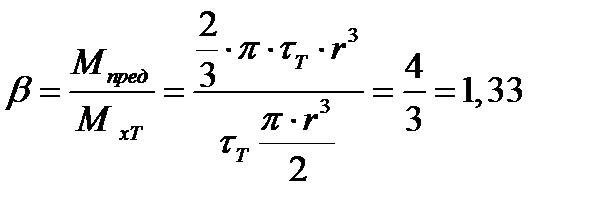показывает, что от момента первого появления пластических деформаций до полного исчерпывания несущей способности крутящий момент должен возрасти в 1,33 раза. Другими словами, 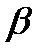выражает резерв несущей способности стержня за счет упругопластических свойств материала.