Модифицированные критерии подобия

В ряде случаев оказывается затруднительным или даже невозможным определить или вычислить ту или иную физическую величину, входящую в критерий подобия. Тогда эту величину исключают путем сочетания двух или более критериев. В результате такой операции получают так называемый производный критерий подобия.При этом исключенную величину обычно заменяют на другую, ей пропорциональную, опытное или расчетное определение которой является наиболее простым.

Так, например, в процессе теплообмена в условиях естественной конвекции, возникающей под действием разности плотностей жидкости, обусловленной различием температур в разных ее точках, трудно определить скорость конвективных токов. Однако эта скорость входит в критерий Фруда, отражающий подобие таких процессов. Поэтому неизвестная скорость в процессе может быть исключена путем сочетаниякритериев Рейнольдса и Фруда:

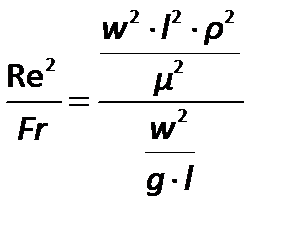
(2.82)

Полученный комплекс величин является производным критерием, называемым критерием Галилея:

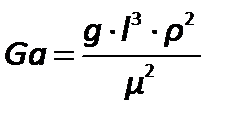
(2.83)

Можно получить другой производный критерий – критерий Архимеда, представляющий собой критерий Галилея, умноженный на симплекс физического подобия–безразмерную плотность:

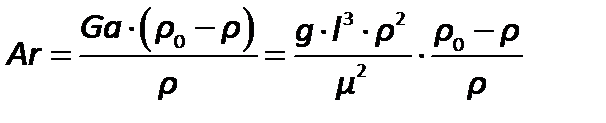
(2.84)

Если заменить симплекс 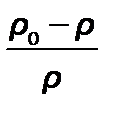пропорциональной ему относительной разностью температур, то можно получить новый производный критерий, являющийся критерием теплового подобия Грасгофа.

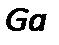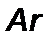Соблюдение равенства критериев или является необходимым при моделировании различных процессов, протекающих под действием силы тяжести.