Уравнения фильтрования

Скорость процесса фильтрования пропорциональна движущей силе и обратно пропорциональна сопротивлению процесса:

,

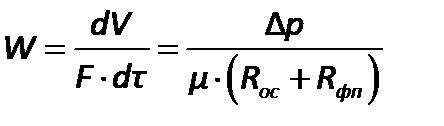(2.194)

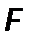где - объем фильтрата; - поверхность фильтрования; 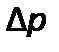- разность давлений; 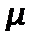-вязкость жидкойфазы суспензии; 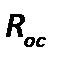- сопротивление осадка; 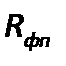- сопротивление фильтровальной перегородки.

Разность давлений 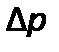может быть создана при повышении давления над фильтровальной перегородкойили созданием вакуума под ней. В этой связи различают фильтры, работающие под давлением, и фильтры, работающие под вакуумом. Схема фильтра, в котором процесс осуществляется под действием перепада давления с отложением осадка, приведена нарис. 2.45.

Рис. 2.45. Схема фильтра: 1 – емкость; 2 – фильтрующая ткань; 3 – дренажная сетка;4 – опорная решетка; I – cуспензия;II – осадок;III – фильтрат

Теория фильтрования основана на предположении о том, что в капиллярах осадка движение жидкости носит ламинарный характер.

По мере увеличения количества фильтрата, пропущенного фильтром, высота слоя осадка на его поверхности увеличивается. Это приводит к увеличению сопротивления 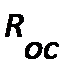.Величину 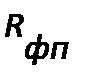можно считать приблизительно постоянной, пренебрегая при этом некоторым возможным ее увеличением вследствие проникновения в поры перегородки твердых частиц. Если величину 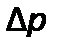поддерживать постоянной, то, как видно из уравнения, скорость фильтрования будет уменьшаться. Такой режим фильтрования называется фильтрованием при постоянном давлении.

Для интегрирования уравнения необходимо установить зависимость между сопротивлением слоя осадка и объемом полученного фильтрата. Введем следующие обозначения: 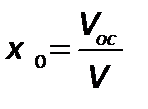; 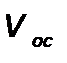- объем осадка.

Тогдавысота слоя осадка равна

,

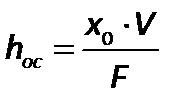(2.195)

а сопротивление слоя осадка можно выразить равенством

,

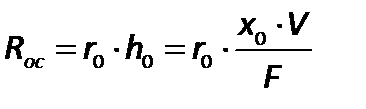(2.196)

где 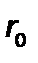- удельное сопротивление слоя осадка.

Из этого равенства следует, что величина 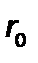характеризует сопротивление, оказываемое потоку жидкой фазы равномерным слоем осадка толщиной 1 м.

Подставив значение 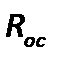в зависимость скорости процесса, получим

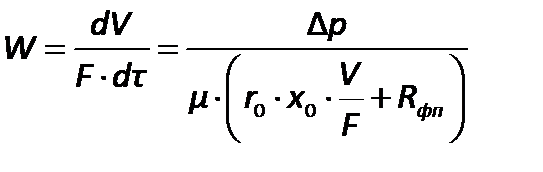
(2.197)

Если принять, что сопротивлением фильтровальной перегородки можно пренебречь, из предыдущего равенства получим

.

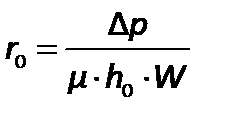(2.198)

При динамическом коэффициенте вязкости 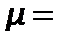1 Па∙с, высоте осадка 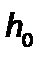=1 м и скорости фильтрования 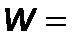1 м/с удельное сопротивление осадка .

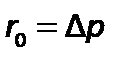Таким образом, удельное сопротивление осадка численно равно разности давлений, необходимой для того, чтобы жидкая фаза с вязкостью равной единице фильтровалась со скоростью 1 м/счерез слой осадка толщиной1 м.

Жидкость с такой большой вязкостью может существовать только гипотетически. В связи с этимна практике такой большой разности давлений быть не может. Для сильно сжимаемых осадков значение 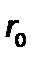достигает10¹² м^-2 и более.

Если принять 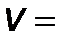0, что соответствует началу процесса фильтрования, когда на фильтровальной перегородке еще не образовался слой осадка, из уравнения для скорости фильтрования получим

.

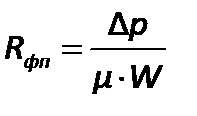(2.199)

При динамическом коэффициенте вязкости 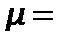1 Па∙си скорости фильтрования 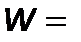1 м/с сопротивление фильтровальной перегородки 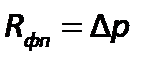. Это означает, что сопротивление фильтровальной перегородки численно равно разности давлений, необходимой для того, чтобы жидкая фаза с вязкостью равной единице проходила через фильтровальную перегородку со скоростью1 м/с. Для ряда фильтровальных перегородок величина 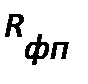имеет порядок10¹⁰ м ^-1.

При постоянной разности давлений и неизменной температуре фильтрата, фильтра конкретной конструкции и установленных параметров фильтровальной перегородки все входящие в уравнение фильрования величины постоянны, за исключением получаемого на фильтре объема фильтрата и времени 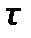. Проинтегрируем это уравнение в пределах от 0 до и от 0 до :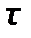

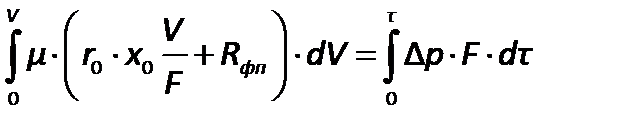
(2.200)

или

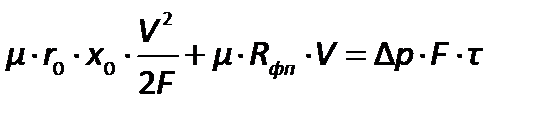
(2.201)

Уравнение показывает зависимость продолжительности фильтрования от объема фильтрата. При решении его относительно можно получить зависимость объема получаемого фильтрата от продолжительности фильтрования. Это уравнение применимо к сжимаемым и несжимаемым осадкам. Постоянную разность давлений можно создавать двумя способами: или пространство над фильтровальной перегородкой сообщают с источником сжатого воздуха, или пространство под фильтровальной перегородкой присоединяют к источнику вакуума. Обычно такие процессы осуществляют в так называемых нутч-фильтрах.

В процессе фильтрования при постоянной скоростисуспензию на фильтр подают поршневым насосом, производительность которого при заданном числе оборотов постоянна. В этой связи производную 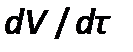можно заменить отношением конечных величин и

.

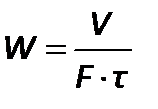(2.202)

Уравнение для скорости имеет вид

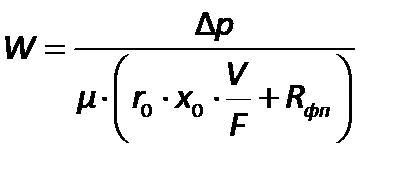
(2.203)

Решим это уравнение относительно разностидавлений 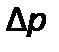, значение которой меняется с увеличением высоты осадка:

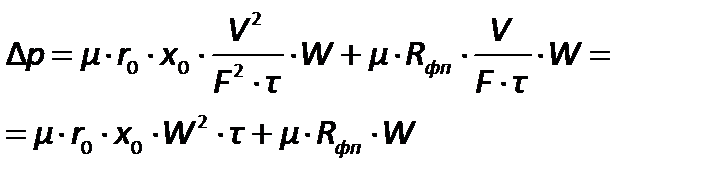
(2.204)

Из уравнения следует, что разность давлений возрастает по мере увеличения продолжительности процесса. Это уравнение применимо к несжимаемым осадкам. При использовании его для сжимаемых осадков следует иметь аналитическую зависимость удельного сопротивления осадка от разности давлений.

Фильтрование при постоянных разности давлений и скоростиосуществляется при прохождении чистой жидкости в процессе промывки осадка на фильтре способом вытеснения.

Для расчета объема промывной жидкости, подаваемой на фильтр при и , из уравнения фильтрования получим

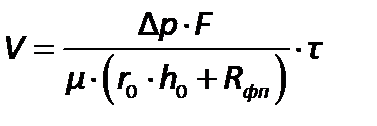
(2.205)

Это уравнение применимо для сжимаемых и несжимаемых осадков,поскольку в процессе фильтрования .