ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПОВЕРХНОСТЬЮ

Возможны три варианта расположения прямой относительно поверхности. Прямая может:

1) пересекать поверхность;

2) касаться поверхности;

3) не пересекать поверхность.

Частные случаи:

Пример 1. Пересекаются прямая общего положения l с проецируюей поверхностью F (рис9.1).

Если задана проецирующая поверхность, то одна из проекций искомых точек пересечения определяется сразу, исходя из принадлежности их этой проецирующей поверхности.

В данном примере призма является горизонтально-проецирующей поверхностью, следовательно, горизонтальные проекции точек пересечения лежат на пересечении горизонтальной проекции прямой l и горизонтального очерка призмы.

.

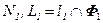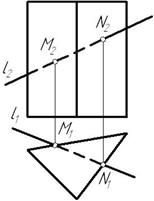
Рисунок 9.1. Пересечение прямой с призмой

Вторая проекция точек определяется исходя из принадлежности их непроецирующей прямой l.

.

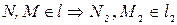Пример 2. Пересекаются проецирующая прямая i с поверхностью конуса F (рис.9.2).

В этом случае одна из проекций искомой точки также изначально определена на чертеже. Она совпадает с вырожденной проекцией прямой.

.

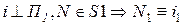Вторая проекция точки определяется из условия принадлежности ее образующей поверхности.

.

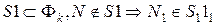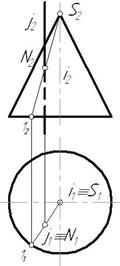
Рисунок 9.2. Пересечение прямой с конусом

Общий случай:

Пересекаются непроецирующая поверхность и прямая общего положения.

В этом случае, чтобы найти точки пересечения прямой с поверхностью, необходимо:

1) Заключить прямую в дополнительную (вспомогательную) плоскость.

2) Построить линию пересечения вспомогательной плоскости с поверхностью.

3) Определить точки пересечения полученного сечения с заданной прямой.

Эти точки являются искомыми.

В качестве вспомогательной плоскости выбирают плоскость общего или частного положения, дающую наиболее простую линию сечения поверхности (ломаную или окружность).

Пример: Построить точки пересечения прямой l с трехгранной пирамидой SABC. Определить видимость прямой относительно поверхности (рис.9.3).

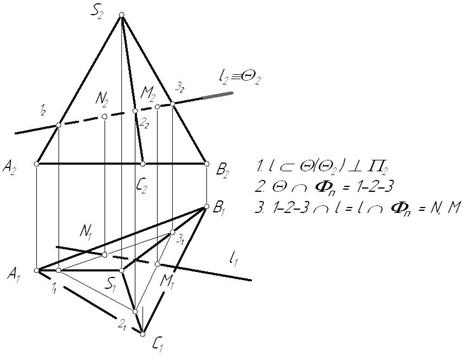
Рисунок 9.3. Пересечение прямой с пирамидой

Видимость прямой определяется по принадлежности точек пересечения граням пирамиды. Видима та часть прямой, которая исходит из точки, лежащей на видимой грани многогранника.