и оптимизация механизма

В соответствии с разработанным планом осуществляется моделирование механизма АКУ, определяются для каждого опыта значения функции j(…), после чего рассчитываются коэффициенты линейной модели.

Далее реализуется метод пошаговой оптимизации (Бокса-Уилсона, крутого восхождения).

Напомним, метод пошаговой оптимизации состоит в последовательном движении по градиенту функции j(…). При этом факторы (в их натуральном выражении!) получают приращения, начиная от нулевого уровня, в соответствии с соотношениями:

Dх_i=±b_iJ_ia,

где а – множитель, позволяющий пропорционально уменьшить или увеличить значения приращений факторов; знак «+» или «-» ставится в зависимости от того, каков знак рассчитанного коэффициента b_i при факторе (например, если коэффициент b_i<0, то следовательно для движения к экстремуму необходимо уменьшать значения фактора, и знак должен быть «-»).

При выборе коэффициента а требуется внимательность. Дело в том, что приращения факторов не должны быть большими, чтобы не «проскочить» экстремум. При этом малые приращения увеличивают количество шагов и время моделирования. Таким образом, при выборе масштабного множителя а необходимо увязать два этих противоречия.

В результате реализации построенного плана и последующей пошаговой оптимизации получены значения параметров механизма, которые можно считать наилучшими. Эти значения следующие:

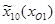=427,4; 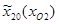=602;

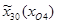=1421,6; 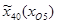=1593,2;

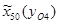=-74,8; 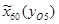=-148,3;

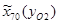=-144; 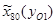=-75,6;

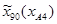=51,9; 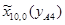=-104,8;

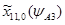=0,27; 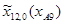=1049,6;

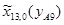=-104,8; 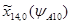=0,232;

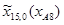=1635,9; 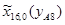=-84,2;

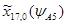=0,555.

Еще раз отметим особенность данного механизма, о которой уже упоминалось: очень высокая чувствительность к малейшему изменению его параметров.

Важно также понимать, реализация плана эксперимента осуществляется по отношению к математической модели механизма, описывающей взаимодействие его элементов, их скорости и ускорения на основе принципов теории механизмов и машин.