Классическая постановка задачи оптимизации

Общая задача математического программирования формулируется следующим образом: найти вектор 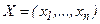удовлетворяющий системе ограничений

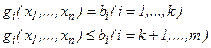
и доставляющий экстремум функции .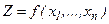

Т.е.

В некотором пространстве 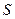тем или иным способом выделяется некоторое непустое множество 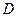точек этого пространства, называемое допустимым множеством. Далее фиксируется некоторая вещественная функция 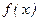, заданная во всех точках 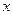допустимого множества. Она называется целевой функцией. Задача оптимизации состоит в том, чтобы найти точку 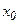в множестве 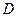, для которой функция 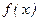принимает экстремальное – максимальное или минимальное значение.

При перемене знака целевой функции 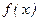все точки ее максимума превращаются, очевидно, в точки минимума и наоборот. Поэтому в теории достаточно рассматривать лишь какой-либо один из видов оптимума (максимум или минимум). В современной теории оптимизации чаще всего останавливаются на задаче нахождения минимума, или, что-то же самое, на задаче минимизации функций. Все результаты этой задачи очевидным образом переносятся и на задачу нахождения максимума.

Обычно на некоторые переменные 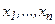накладывается условие неотрицательности. Кроме того, ограничением может служить условие целочисленности решения для ряда переменных.