Метод итераций и метод Зейделя

Метод итераций позволяет получить последовательность приближенных значений, сходящуюся к точному решению системы линейных уравнений. В отличие от метода Гаусса, метод итераций не требует контроля промежуточных вычислений, так как отдельные ошибки на каком-либо шаге итерации не искажают окончательных результатов, хотя и удлиняет процесс счета. Иначе говоря, метод итераций решения систем линейных уравнений является самоисправляющимся. Кроме того, метод итераций легко запрограммировать для ЭВМ. Пусть имеем систему

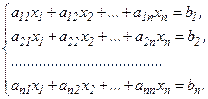
или, короче,

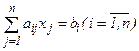. (3.8)

Предположим, что определитель системы отличен от нуля и что диагональные коэффициенты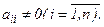

Выразим из первого уравнения 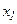, из второго 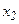, и т. д. Тогда получим эквивалентную систему:

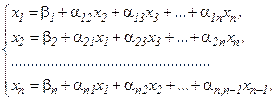
где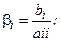

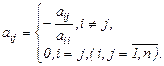
Полученную систему запишем так:

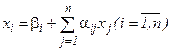(3.9)

и назовем ее системой нормального вида.

Будем решать ее методом последовательных приближений. За нулевое приближение возьмем, например, столбец свободных членов

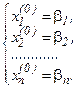
Подставив в правую часть системы (3.9) значения 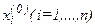, получим первое приближение:

.

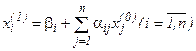Затем аналогично второе: 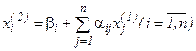и т.д.

Таким образом, зная 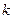-e приближение, ( 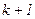)-е приближение вычисляют по формуле:

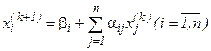(3.10)

Если последовательность приближений 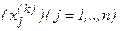имеет предел

то 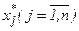является точным решением системы нормального вида, а значит, и исходной системы. В самом деле, переходя к пределу при 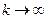в (3.10), имеем:

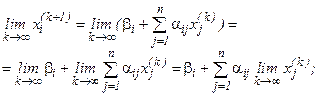
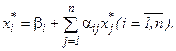
Описанный метод последовательных приближений называется методом итераций. Рабочие формулы метода итераций имеют вид:

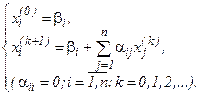(3.11)

Существование предела

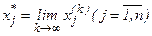
гарантирует теорема о достаточном признаке сходимости процесса итераций.

Достаточным условием сходимости итерационных методов является условие

(3.12)

При методе Зейделя итерационный процесс подобен описанному для метода простых итераций, однако уточненные значения 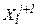сразу подставляются в последующие уравнения. Формула итерационного процесса имеет вид:

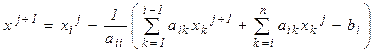
Контрольные вопросы

1. К какому виду преобразуют исходную систему для применения метода итераций?

2. В чем преимущество метода итераций перед другими методами?

3. Каковы условия применимости данного метода?

4. Какова скорость сходимости последовательности векторов к решению?

5. Сформулируйте условие окончания вычислений в методе простых итераций?

6. Какова общая постановка задачи решения систем линейных уравнений?

7. Что такое ранг матрицы?

8. Сформулируйте условие существования решения и условие единственности решения.

9. Что такое эквивалентное преобразование системы? Какие они бывают?

10. Почему при добавлении к строке линейной комбинации других строк решение не меняется?

11. С чем связана необходимость переставлять местами уравнения системы при решении?

12. Когда целесообразно применять метод Гаусса?

13. Какова цель прямого хода в методе Гаусса?

14. Как выполняется обратный ход метода Гаусса?

15. На каком ходе, прямом или обратном, необходимо учитывать условия применения метода Гаусса?

16. Объясните алгоритм схемы единственного деления.

17. Объясните алгоритм схемы с частичным выбором ведущего коэффициента по столбцу.

18. Расскажите о достоинствах и недостатках схемы с полным выбором ведущего коэффициента.

19. Объясните зависимость временных затрат от размера системы.

20. Объясните зависимость ошибок от размера системы.

21. Когда система линейных алгебраических уравнений имеет единственное решение?

22. Каковы недостатки решения системы уравнений по правилу Крамера?

23. Охарактеризуйте точные и приближенные численные методы решения систем линейных алгебраических уравнений.

24. Опишите метод Гаусса с выбором главного элемента.

25. Почему метод простой итерации называется самоисправляющимся?

26. Дайте определение сходимости итерационного процесса.

27. Опишите метод Зейделя.

28. Точные методы решения систем линейных уравнений

29. Приближенные методы решения систем линейных уравнений

30. Правило Крамера.