Безусловная оптимизация

Классическая теория экстремумов функции дает признаки абсолютного и относительного, условного и безусловного максимума (минимума):

В классической теории оптимизации различают необходимые и достаточные условия существования экстремума.

Рассмотрим сначала необходимые условия в случае функции одной переменной.

Рассмотрим функцию двух переменных. Если функция f(x,y) в точке (х₀, у₀) имеет экстремум, то в этой точке либо обе ее частные производные первого порядка равны нулю 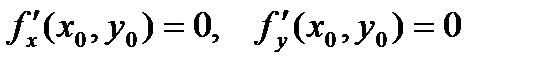, либо хотя бы одна из них не существует. Эту точку (х₀, у₀) будем называть критической точкой.

Пусть в окрестности критической точки (х₀, у₀) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение:

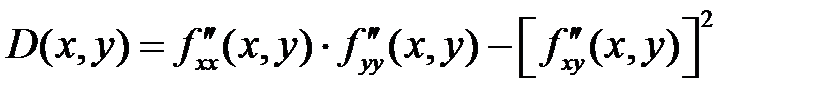
- Если D(x₀, y₀) > 0, то в точке (х₀, у₀) функция f(x, y) имеет экстремум, если 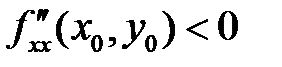- максимум, если 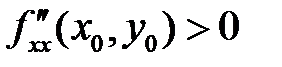- минимум.

- Если D(x₀, y₀) < 0, то в точке (х₀, у₀) функция f(x, y) не имеет экстремума. В случае, если D = 0, вывод о наличии экстремума сделать нельзя.

Аналогично данные положения можно обобщить для n переменных. Необходимым условием существования экстремума в точке 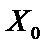является равенство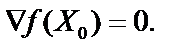

Пример

Например, градиент функции 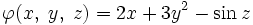будет представлять собой:

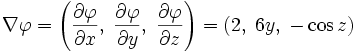
К стационарным точкам относятся не только точки относительного (локального) экстремума, но и седловые точки (рис.3).

точка относительного (локального) экстремума

седловая точка

Рис..3. Стационарные точки

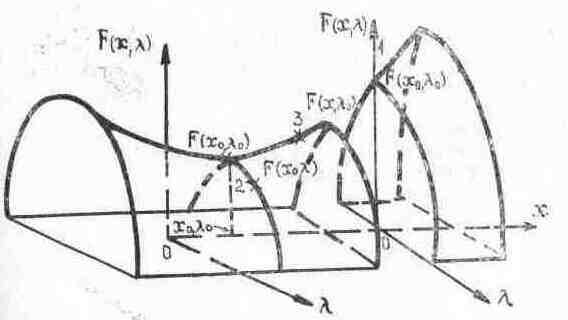
Для W(j₁, j₂) седловая точка – это такая точка j^* =(j₁^*, j₂^*) в которой целевая функция W(j₁, j₂) принимает наименьшее значение по одной координате j₁ и наибольшее значение по другой координате j₂. В окрестности седловой точки для любых значений j₁, j₂ всегда выполняется: W(j₁^*, j₂) £W(j₁^*, j₂^*) £W(j₁, j₂^*).

На рисунке приведены примеры задачи оптимизации функции двух переменных при отсутствии ограничений.

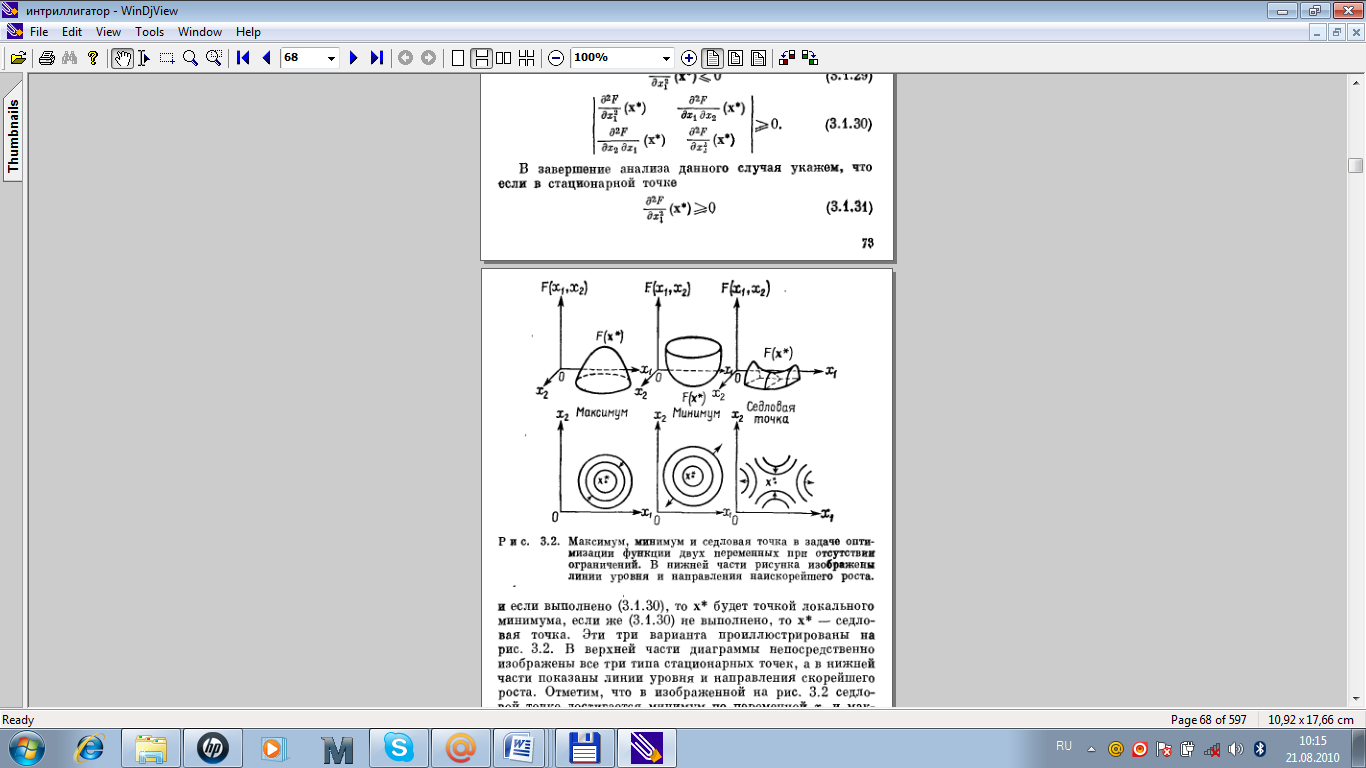
Достаточным условием существования безусловного относительного экстремума функции W(j) является то, чтобы матрица Гессе Нв точке j⁰ (Н|_j⁰) была либо положительно определенной (тогда j⁰ – точка минимума), либо отрицательно определенной (тогда j⁰ – точка максимума).

Матрица Гессе Несть матрица вторых производных W(j). С помощью данной матрицы исследуется знак квадратичной формы 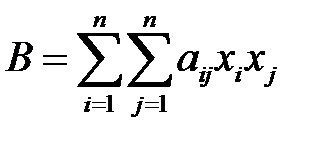, коэффициенты которой определяются соотношениями

.

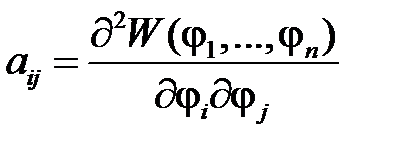Квадратичная форма может быть положительно и отрицательно определенной. Ответ о знаке квадратичной формы дает теорема, которая формулируется следующим образом. Для положительной определенности квадратичной формы необходимо и достаточно, чтобы были выполнены условия Сильвестра – все главные миноры матрицы должны быть строго положительны.

Например, для W(j₁, j₂, j₃)= j₁+2j₃+j₂j₃–j₁²–j₂²–j₃² матрица Гессе Н|_j⁰ имеет вид:

,

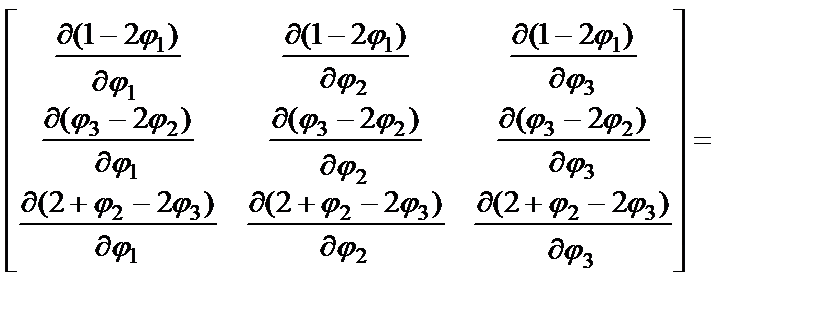
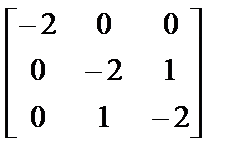т. к. необходимое условие экстремума ÑW(j⁰)=0, то

¶W/¶j₁ =1–2j₁ = 0, ¶W/¶j₁ = j₃–2j₂ = 0, ¶W/¶j₁ = 2+j₂–2j₃ = 0.

Для того, чтобы матрица Гессе Н|_j⁰ была положительно определенной (все ее собственные значения были положительны), необходимо и достаточно, чтобы все k-е главные миноры Δ_k матрицы были положительны. Для того, чтобы неособенная квадратная матрица Гессе Н|_j⁰ была положительно полуопределенной необходимо и достаточно, чтобы все k-е главные миноры Δ_k матрицы были положительны или равны нулю.

Для того чтобы матрица Гессе Н|_j⁰ была отрицательно определенной (все ее собственные значения были отрицательны), необходимо и достаточно, чтобы k-е главные миноры Δ_k матрицы были отличны от нуля и имеют знак (–1)^k, k=1, 2, …,n. Для того чтобы неособенная квадратная матрица Гессе Н|_j⁰ была отрицательно полуопределеннойнеобходимо и достаточно, чтобы k-е главные миноры Δ_k матрицы были равны нулю или имели знак (–1)^k, k=1, 2, …,n.

Во всех остальных случаях, когда знаки главных миноров не удовлетворяют комбинациям, описанным выше, матрица Гессе Н|_j⁰ является неопределенной.

Главным минором Δ_k неособенной квадратной матрицы называется определитель, образованный элементами, стоящими на пересечении k выделенных строк матрицы и k выделенных столбцов матрицы, причем номера выделенных строк и столбцов матрицы совпадают.

Так, в нашем примере Δ1 и Δ3 – отрицательны, Δ2 - положительный:

Δ1=a11=–2; Δ2=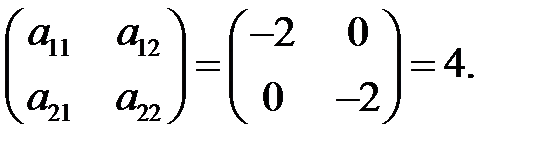

Δ3=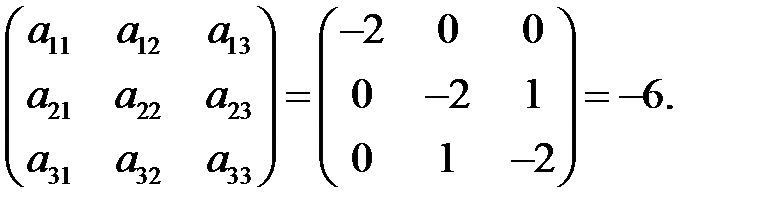

Таким образом, матрица отрицательно определена.