Понятие погрешности

Различают два вида погрешностей - абсолютную и относительную. Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения. Относительная погрешность - это отношение абсолютной погрешности к истинному значению числа.

Абсолютной погрешностью приближенного числа а назовем величину ∆а, про которую известно, что .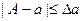

Таким образом, точное число заключено в границах 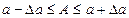или сокращенно .

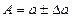Пример 1:Приближенные числа 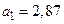; ; 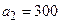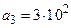получены округлением, точные значения чисел неизвестны. Что можно сказать об абсолютной погрешности данных приближенных чисел?

Решение:Пользуясь правилами округления чисел, можно сказать, что абсолютные погрешности приближенных чисел не превосходят половины единицы последнего разряда, т.е.

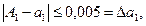
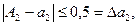
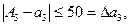
Для приближенного числа, полученного в результате округления, абсолютная погрешность 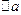принимается равной половине единицы последнего разряда числа.

Пример 2: Значение 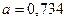могло быть получено округлением чисел 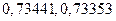и др. При этом 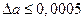, и полагаем .

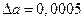При вычислениях на ЭВМ округления, как правило, не производятся, а цифры, выходящие за разрядную сетку машины, отбрасываются. В этом случае максимально возможная погрешность результата выполнения операции в два раза больше по сравнению со случаем округления.

Абсолютная погрешность связана с размерностью и не полностью характеризует результат. Например, известно, что абсолютная погрешность равна 3 см. Ясно, что имеем совершенно различный по точности результат, если речь идет о длине карандаша или о расстоянии между Землей и Сатурном. Поэтому вводят понятие относительной погрешности.

Относительной погрешностью 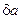приближенного числа 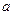называется отношение абсолютной погрешности 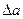к абсолютной величине приближенного числа :

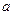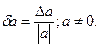
Для приближенного числа, полученного в результате округления, абсолютная погрешность 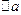принимается равной половине единицы последнего разряда числа. Например, значение 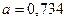могло быть получено округлением чисел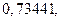 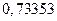и др. При этом 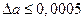, и полагаем .

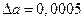Приведем примеры оценки абсолютной погрешности при некоторых значениях приближенной величины 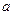(таб. 1.1).

Таблица 1.1 - Оценка абсолютной погрешности

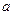
	51,7	-0,0031		16,00
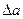
	0,05	0,00005	0,5	0,005

При вычислениях на ЭВМ округления, как правило, не производятся, а цифры, выходящие за разрядную сетку машины, отбрасываются. В этом случае максимально возможная погрешность результата выполнения операции в два раза больше по сравнению со случаем округления.

Например: относительная погрешность 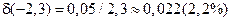. Заметим, что погрешность округляется всегда в сторону увеличения. В данном случае .

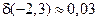Определение 1. Значащими цифрами в десятичной записи числа называются все цифры, начиная с первой ненулевой слева.

Определение 2.Значащая цифра называется верной в узком смысле, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре.

Определение 3. Значащая цифра называется верной в широком смысле, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.

Сформулируем правила округления:

1. если отбрасываемые при округлении цифры составляют число, большее половины единицы последнего оставляемого разряда, то последняя оставляемая цифра увеличивается на единицу;

2. если отбрасываемые при округлении цифры составляют число, меньшее половины единицы последнего оставляемого разряда, то оставляемые цифры остаются без изменения;

3. при округлении, когда отбрасываемые цифры составляют число, равное половине единицы последнего оставляемого разряда, то последняя оставляемая цифра увеличивается на единицу, если она нечетная, и остается без изменения, если она четная (правило четной цифры).