Вычислительная математика и её роль в науке и технике

Вычислительная математика занимается проблемами разработки и исследования вычислительных алгоритмов, их применением к решению конкретных задач.

Слово «Модель» происходит от латинского modus (копия, образ, очертание). Моделирование – это замещение некоторого объекта А (оригинала) другим объектом Б (моделью).

Математическая модель — это упрощенное описание реальности с помощью математических понятий.

Математическое моделирование — процесс построения и изучения математических моделей реальных процессов и явлений, т.е. метод исследования объектов и процессов реального мира с помощью их приближенных описаний на языке математики – математических моделей.

Крупнейшие ученые прошлого сочетали в своих трудах как построение математического описания явлений природы (математические модели), так и его исследования. Анализ усложненных моделей требовал создания новых, как правило, численных методов решения задач.

При решении сложной задачи, она разбивается на ряд простых задач. Процесс решения любой задачи можно представить в виде схемы:

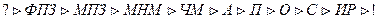
ФПЗ. Физическая постановка задачи. На этом этапе необходимо грамотно поставить задачу, сформулировать и осознать, что же требуется с точки зрения решения проблемы. Для этого необходимо изучить рассматриваемую проблему и обладать знаниями в соответствующей области.

МПЗ. Математическая постановка задачи. На этом этапе нужно переформулировать физическую проблему на математический язык (решение нелинейных уравнений, дифференциальные уравнения, матрицы, статистика и т.п.). Для этого нужно владеть математикой. Далее строится математическая модель. Здесь можно остановиться, т.к. если задача проста, то существуют стандартные методы, которые нужно применить для решения этой задачи.

МНМ. Метод непрерывной математики. Здесь оперируют не с конечными числами, а с функциями, общими величинами и т.п., т.е. ищут решение проблемы в общем виде.

ЧМ. Численные методы (или методы компьютерной (вычислительной) математики). Решение проблемы представляют в виде конечных математических операций – сложение, умножение. Т.е. МНМ сводятся к операциям над числами, в результате которых получается результат.

А. Алгоритмизация. Точное формальное описание процесса. Алгоритмизация служит для упорядочения производимых действий.

П. Программирование. Перевод алгоритма на машинный язык.

О. Отладка. Поиск ошибок, которые могли появиться на предыдущих этапах. Вполне вероятно, что придется вернуться в самое начало, к изменению ФПЗ. Масса итерационных возвратов характерна для любого творческого процесса.

С. Счет - получение рабочих результатов.

ИР. Интерпретация результатов.

В результате исследователь получает в руки универсальный, гибкий и недорогой инструмент, который сначала отлаживается, тестируется и калибруется на решении набора пробных задач. Затем проводится широкомасштабное исследование математической модели для получения необходимых качественных и количественных свойств и характеристик исследуемого объекта.

Предложенная методология получила свое развитие в виде технологии «вычислительного эксперимента».

Вычислительный эксперимент – это информационная технология, предназначенная для изучения явлений окружающего мира, когда натурный эксперимент оказывается либо невозможен (например, при изучении здоровья человека), либо слишком опасен (например, при изучении экологических явлений), либо слишком дорог и сложен (например, при изучении астрофизических явлений).

После проведения первого этапа вычислительного эксперимента может возникнуть необходимость в уточнении модели. На втором этапе учитываются дополнительные эффекты и связи в изучаемом явлении, либо возникает необходимость пренебречь некоторыми закономерностями и связями. Затем этот процесс повторяют до тех пор, пока не убеждаются, что модель адекватна изучаемому объекту.

Численные методы решения задач занимают большое место в практической деятельности инженеров. Для решения задач конкретного типа разрабатывается специальное программное обеспечение, основой алгоритмов которого и служат численные методы.