Особенности машинной арифметики

Знание основных особенностей машинной арифметики необходимо для грамотного использования ЭВМ при численном решении задач.

Будем считать, что все вычислительные машины работают в двоичной системе счисления. Для хранения числа в памяти ЭВМ отводится поле стандартной длины (машинное слово), в котором число записывается в виде последовательности двоичных цифр (0 или 1). Целое число n представляется в виде

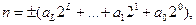(1.3)

где 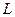- некоторое стандартное для ЭВМ целое число, 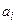– двоичные числа.

Всего для хранения числа 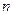отводят 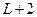разрядов (один из них для хранения знака).

Из представления (1.3) видно, что максимальное по модулю целое число, представимое в ЭВМ, есть 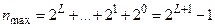. Операции сложения, вычитания и умножения над целыми числами реализованы так, что если результат не превышает по модулю число 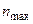, то он получается точным. Однако, если модуль результата превышает 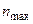, то на ряде вычислительных машин эта ситуация не доводится до сведения пользователя, происходит присвоение результату некоторого значения, меньшего 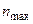по модулю, и вычисления продолжаются далее.

Для вещественных чисел принята форма представления с плавающей точкой, когда каждое число представляется в виде

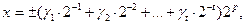(1.4)

где 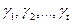– двоичные цифры. Число x нормализуется так, чтобы 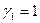и поэтому в ЭВМ хранятся только значащие цифры. Число 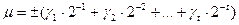называется мантиссой числа 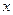. Количество 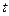цифр, которое отводится для записи мантиссы, называется разрядностью мантиссы, 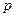- целое число, называемое двоичным порядком. Порядок также записывают, как двоичное целое число 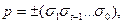для хранения которого в машинном слове отводится 2+l двоичных разрядов.

Так как нуль – ненормированное число (его нельзя представить в виде (1.4) при 0 1 ¹ 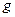), то для его хранения предусматривают особый способ записи.

Отметим следующие моменты:

1. В ЭВМ представимы не все числа, а лишь конечный набор рациональных чисел специального вида. Эти числа образуют представимое множество вычислительной машины. Для всех остальных чисел x возможно лишь их приближенное представление с ошибкой, которую принято называть ошибкой представления (или ошибкой округления). Обычно приближенное представление числа 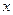в ЭВМ обозначают как 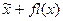. Если округление производят по дополнению, то граница относительной погрешности представления равна единице первого отброшенного разряда мантиссы, т.е 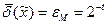. Если же округление производят усечением, то 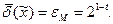Величина 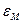играет в вычислениях на ЭВМ фундаментальную роль, ее называют относительной точностью ЭВМ, а также машинной точностью (или машинным эпсилон). Значение этой величины определяется разрядностью мантиссы и способом округления.

Можно считать, что точное число x и отвечающее ему округленное число 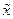связаны равенством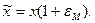

Среди представимых на ЭВМ чисел нет не только ни одного иррационального (в том числе и таких важных постоянных, 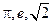), но и даже такого широко используемого в вычислениях числа, как 0,1.

Дело в том, что двоичная запись числа 0,1 является бесконечной периодической дробью: 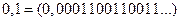. Поэтому это число представляется на ЭВМ приближенно, с погрешностью, вызванной необходимостью округления.

2. Диапазон изменения чисел в ЭВМ ограничен. Для всех представимых на ЭВМ чисел 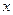(за исключением нуля) имеем: 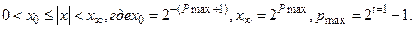Все числа по модулю большие 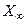рассматриваются, как машинная бесконечность.

Попытка получить такое число приводит к аварийному останову (авосту) ЭВМ по переполнению. Все числа по модулю меньшие 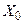для ЭВМ не различимы и представляются, как нуль (машинный нуль). Получение числа x , такого, что 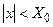, называют исчезновением порядка. Обычно, при исчезновении порядка, автоматически полагается 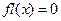и вычисления продолжаются.

3. Правила выполнения арифметических операций в двоичной системе счисления просты и легко реализуются на ЭВМ. Однако в процессе проведения вычислений погрешности округлений (в силу ограниченной разрядности мантиссы арифметические операции над представимыми в ЭВМ вещественными числами не могут быть реализованы точно) могут накапливаться, так как выполнение каждой из четырех арифметических операций вносит некоторую погрешность. Считается, что выполнение каждой арифметической операции вносит относительную погрешность не большую, чем 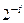Это предположение можно записать в виде: 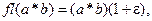(1.5)

где звездочка означает любую из операци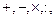й и 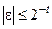. Если результат выполнения арифметической операции является машинным нулем, то в формуле (1.5) надо положить .

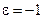Отметим еще раз, что в отличие от обычных математических операций, машинные арифметические операции из-за ограниченной разрядности мантиссы обладают иными свойствами. Например, не выполняется известное правило арифметики «от перемены мест слагаемых сумма не меняется».

Контрольные вопросы

1. Из каких основных этапов состоит процесс решения задачи с помощью ЭВМ? Дайте характеристику каждого этапа.

2. Из каких частей складывается общая погрешность решения задачи? Предмет и задачи численных методов.

3. Основные отличия аналитических и приближенных численных решений.

4. Погрешность как атрибут численных методов.

5. ЭВМ - толчок к стремительному развитию численных исследований.

6. Роль численного анализа в инженерной практике.

7. Что такое абсолютная погрешность приближенного значения величины?

8. Что такое граница абсолютной погрешности?

9. Как с помощью границы абсолютной погрешности ∆x известного приближенного значения х можно указать возможные значения его нижней и верхней границ?

10. Каким образом определяется граница абсолютной ошибки ∆x для приближенного значения х, получаемого в результате многократных измерений?

11. Что такое относительная погрешность приближенного значения величины?

12. Что такое граница относительной погрешности?

13. Как можно вычислить абсолютную погрешность приближения х, если известна его относительная погрешность?

14. Как определить количество верных значащих цифр результата вычислений.

15. Чему равны погрешности суммы, разности, произведения, частного, степени и корня.

16. Какие цифры в записи приближенного числа называются верными в широком смысле, а какие верными в строгом смысле?

17. Верно ли утверждение, что ЭВМ, округляющая числа по методу отбрасывания, всегда выдает результаты, записанные только верными цифрами? Почему?

18. Какие цифры в записи приближенного числа называются значащими?

19. Что такое округление числа? Что такое погрешность округления?

20. Как различаются погрешности округление методом отбрасывания и симметрическое округление?

21. Из чего складывается полная погрешность округленного числа?

22. Понятие вычислительного алгоритма.

23. Приближенное значение величины.

24. Верные, значащие, сомнительные цифры числа.

25. Погрешности арифметических действий.