Построение ЛАХ в низкочастотном диапазоне

На низкочастотном участке, где вид 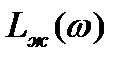определяется в основном требованиями к точности регулирования, а следовательно, величиной коэффициента усиления системы, порядком ее астатизма, значением коэффициента ошибки и т.д.

Если в системе, отрабатывающей ступенчатый входной сигнал 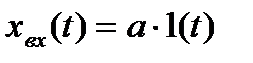, допустимая статическая ошибка не должна превышать значения 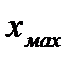, то в соответствии с выражением (5.2) величина коэффициента усиления разомкнутой скорректированной системы:

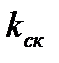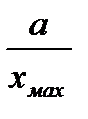≥ – 1.

При этом на участке низких частот желаемая ЛАХ проводится параллельно оси абсцисс с ординатой 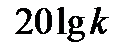. В случае, когда статическая ошибка недопустима ( 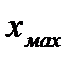= 0), то скорректированная система должна быть астатической.

Если в астатической системе с астатизмом первого порядка требуется обеспечить слежение за сигналом 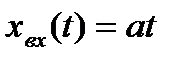, то ее коэффициент усиления, согласно выражению (5.2) определяется величиной максимально допустимой ошибки по скорости :

≥ .

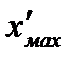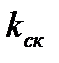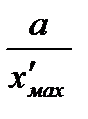При этом уравнение низкочастотного участка желаемой ЛАХ:

.

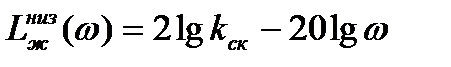При синтезе следящих систем, входной сигнал которых заранее неизвестная функция времени, обычно указываются только максимально возможные значения скорости ( 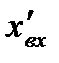) и ускорения ( 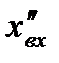) входного сигнала и задаются требованием к величине максимально допустимой динамической ошибке регулирования ( 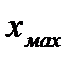). В этом случае подбирается эквивалентное гармоническое воздействие 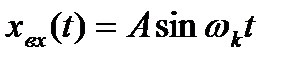, амплитуда и частота которого определяется значениям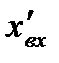и 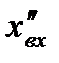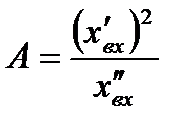и :

и 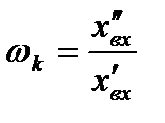. (7.3)

При воспроизведении линейной следящей системой эквивалентного гармонического воздействия ошибка регулирования также будет гармонической с той же частотой 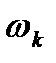и амплитудой 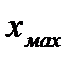. Следовательно:

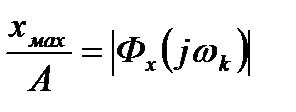, т.е. .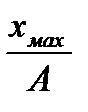

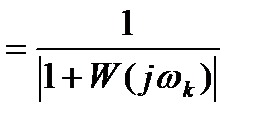Полагая 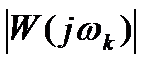>> 1, имеем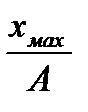 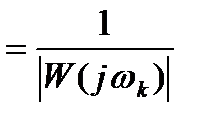, откуда с учетом выражения (7.3):

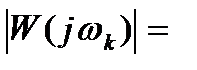
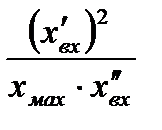
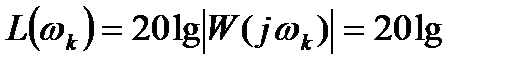
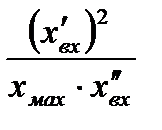. (7.4)

Запретная область

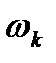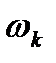
-20 дБ/дек

-40 дБ/дек

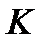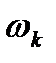
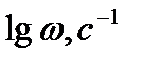
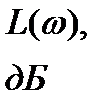
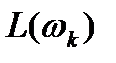
Рис. 7.2. К определению запретной области для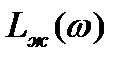

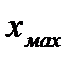Из выражения (7.4) следует, что эквивалентное входное воздействие будет воспроизводиться следящей системой с ошибкой, не превышающей , если при 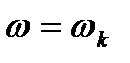ордината желаемой ЛАХ будет не менее

.

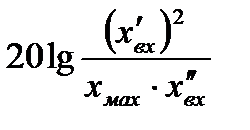Точку К с координатами ( 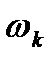; 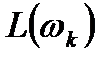) называют контрольной точкой(рис. 7.2). На этом рисунке указаны две прямые, пересекающиеся в точке К, имеющие наклон -20 дБ/дек при 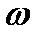< 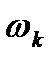и -40 дБ/дек при 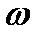> 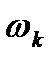. Уравнения этих прямых получены на основании выражения (7.4) при уменьшении скорости и ускорения входного сигнала по отношению к их максимально возможным значениям. Данные прямые представляют собой границы запретной зоны для желаемой ЛАХ следящей системы с астатизмом первого порядка.