Метод последовательного программирования

Для построения схем пере­менных состояния способом последовательного программирования передаточная функция (6.9) в зависимости от числа и вида ее нулей и полюсов должна быть представлена в виде последовательного соединения элементарных звеньев с передаточ­ными функциями вида:

; ; ;

; .

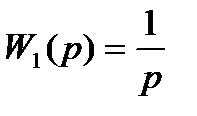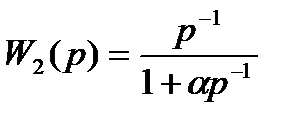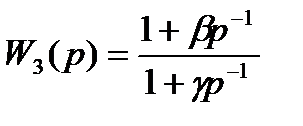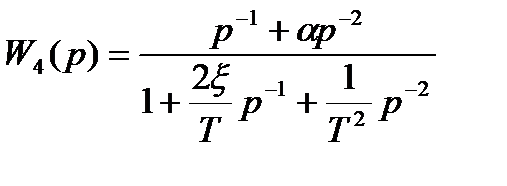В качестве переменных состояния также выбираются выходные величины интегрирующих звеньев, выходной сигнал системы 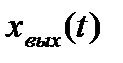в этом случае обычно совпадает с переменной состояния последнего звена.

В качестве примера рассмотрим описание в пространстве состояния системы (рис. 6.5).

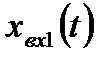
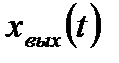
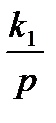
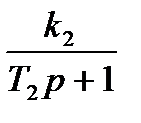
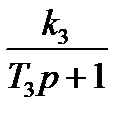
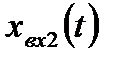
Рис. 6.5. Исходная структура САУ

На основании метода последовательного программирования составим схему переменных состояния этой системы (рис. 6.6).

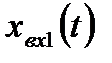
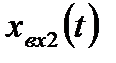
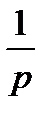
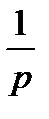
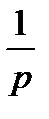
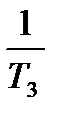
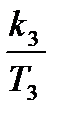
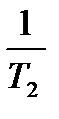
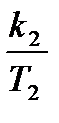
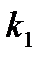
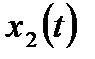
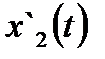
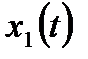
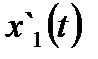
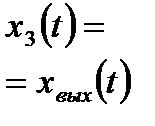
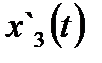
Рис. 6.6. Структура САУ для переменных состояния

Поскольку в качестве переменных состояния выбираются выходные величины интегрирующих звеньев, производные по времени этих переменных состояния представляют собой входные сигналы соответствующих интеграторов. При этом система дифференциальных уравнений (6.2) для рассматриваемой САУ имеет следующий вид:

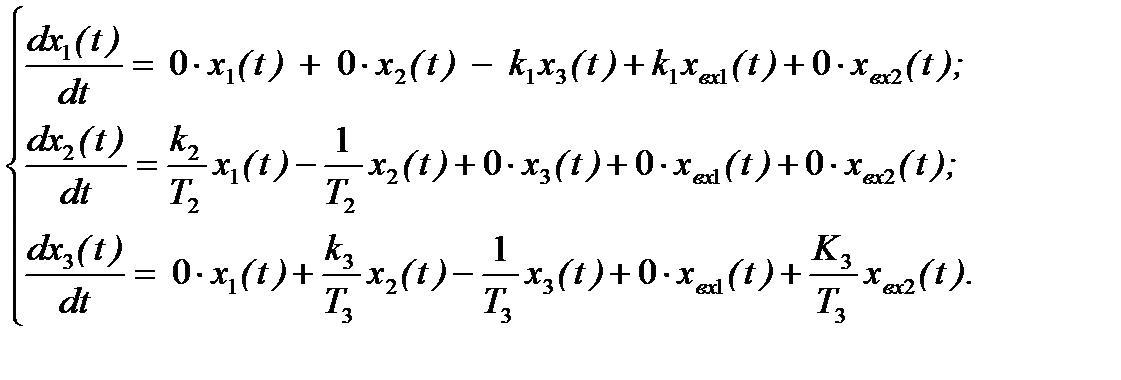(6.13)

Кроме того, 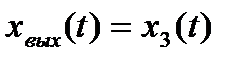или

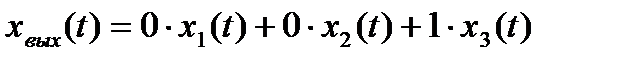. (6.14)

Тогда выражения (6.13) и (6.14) в матричной форме примут вид:

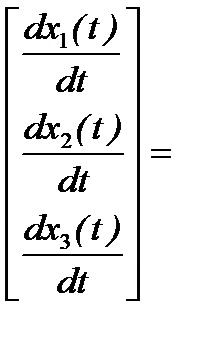
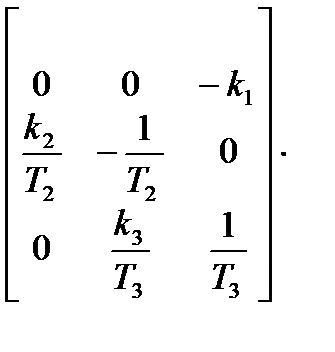
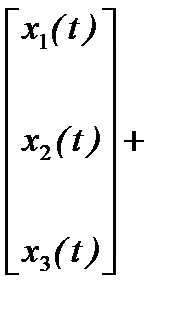
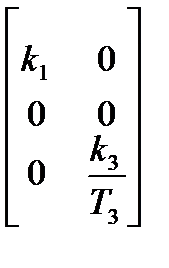
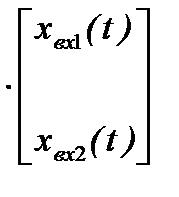
и ,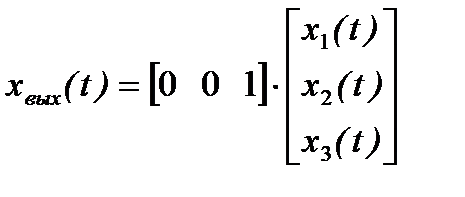

т.е. для рассматриваемой САУ:

матрица системы A = 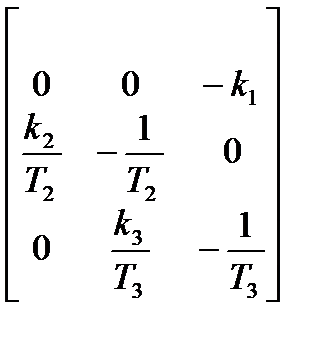, матрица управления B =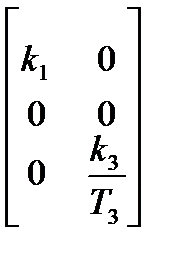

и матрица наблюдения .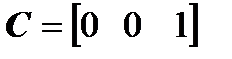

6.3. Решение уравнений состояния
линейных стационарных САУ.
Вычисление фундаментальной матрицы

Рассмотрим методику решения уравнения состояния линейной стационарной системы, находящейся в свободном движении. При этом внешние воздействия на систему не действуют ( X_вх(t)= 0 ) и поведение системы описывается однородным векторным дифференциальным уравнением:

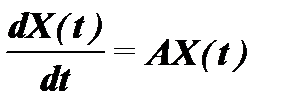. (6.15)

Решение этого уравнения ищем в виде:

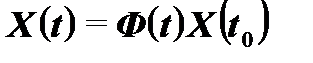, (6.16)

где Ф(t) – фундаментальная матрица;X(t₀) – вектор, описывающий состояние системы в начальный момент времени t₀ .

Для стационарных линейных САУ решение матричного уравнения (6.15) можно получить по аналогии с решением скалярного дифференциального уравнения в виде:

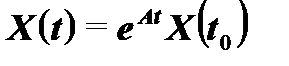, (6.17)

где 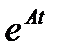– матричная экспонента.

Из сравнения выражений (6.16) и (6.17) следует, что фундаментальная матрица равна:

Ф(t) = exp(At). (6.18)

Существует несколько способов определения фундаментальной матрицы.

Первыйспособ основан на известном разложении экспоненты в ряд. Для выражения (6.18) такое разложение принимает вид:

exp(At) = 1 + ,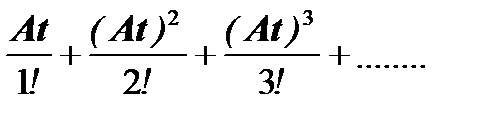

где 1 – единичная матрица.

Указанный способ определения фундаментальной матрицы обычно используется при численных расчетах для фиксированного момента времени t = t₀.

При этом

exp(At₀) = 1 + At₀ + A² + A³ +…….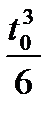

Вычисление подобного выражения для электронных вычисли­тельных машин является стандартной задачей, не представляющей каких-либо затруднений даже для систем высокого порядка.

Второй способ вычисления фундаментальной матрицы предполагает использование аналитического выражения для Ф(t). Для его определения выполним преобразование Лапласа над обеими частями матричного дифференциального уравнения (6.15):

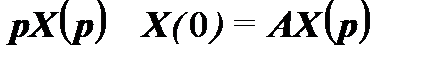или ,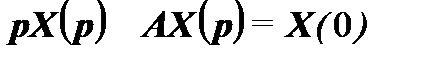

откуда

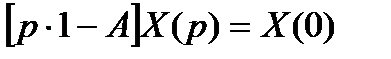. (6.19)

Матрица [р1 – А] называется характеристической матрицей, ее определитель

det[p1-A] = 0

представляет собой характеристическое уравнение САУ в матричной форме.

Умножая обе части уравнения (6.19) слева на матрицу [р1 – А]^-1, обратную по отношению к [р1 – А], получим:

X(p) = [р1 – А]^-1 X(0).

Выполнив обратное преобразование Лапласа над последним уравнением, имеем

X(t) = L^-1{[р1 – А]^-1} X(0).

Из последнего выражения следует, что фундаментальная матрица равна:

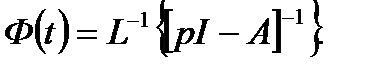(6.20)

В качестве примера определим фундаментальную матрицу системы, передаточная функция которой равна:

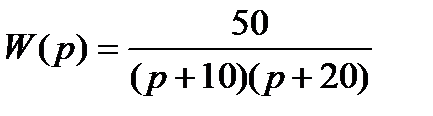. (6.21)

Преобразуем выражение (6.21) к виду:

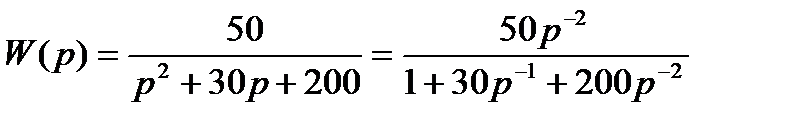. (6.22)

Используя метод прямого программирования, составляем для рассматриваемой системы схему переменных состояния (рис. 6.7), в качестве которых выбираем выходной сигнал системы и его первую производную, т.е. 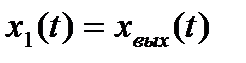, а .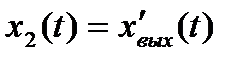

Система дифференциальных уравнений для переменных состояния:

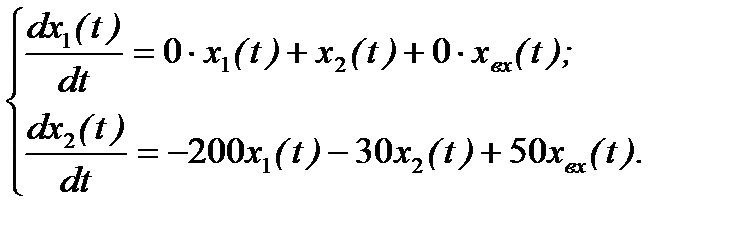
Кроме того, .

Соответствующие приведенной системе дифференциальных уравнений векторные уравнения имеют вид:

= ;

.

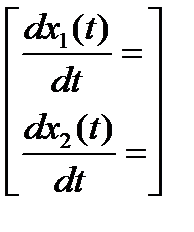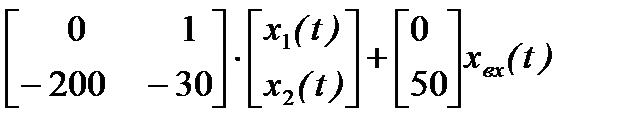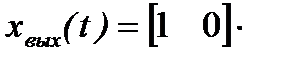
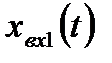
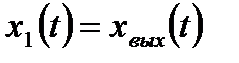
-30

-200

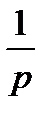
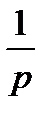
Рис. 6.7. Схема переменных состояния

Таким образом, матрицы системы, управления и наблюдения принимают вид:

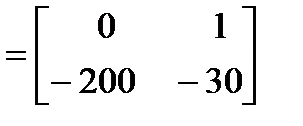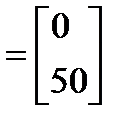A ; B ; C .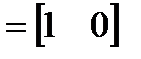

Характеристическая матрица равна:

.

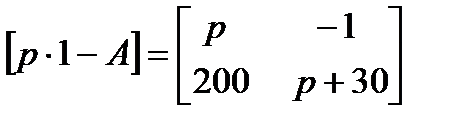Матрица, обратная характеристической, равна:

.

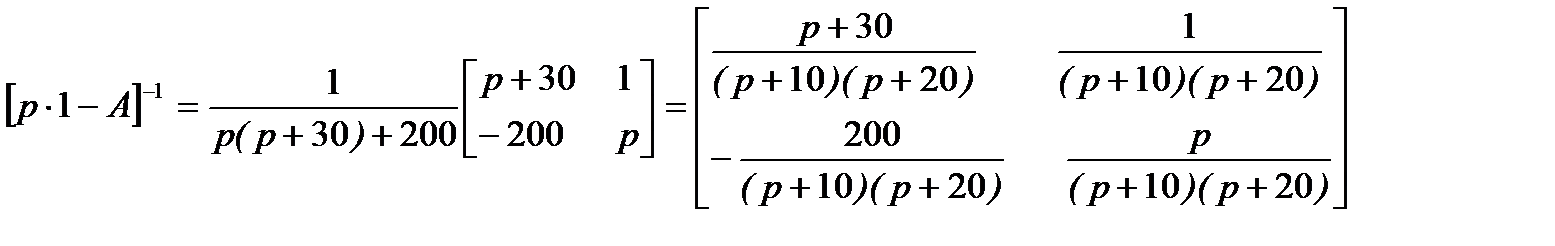В соответствии с выражением (6.20) фундаментальная матрица равна:

= .

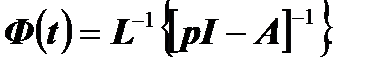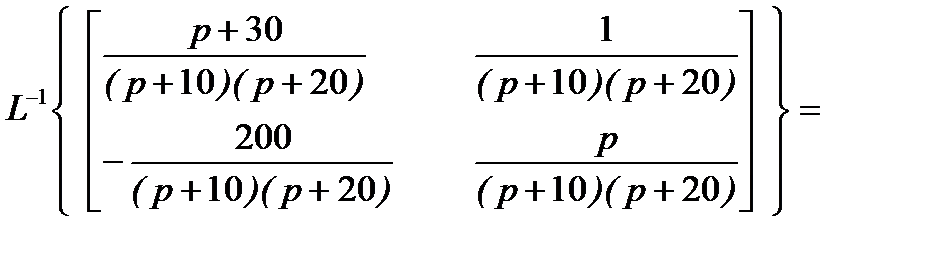
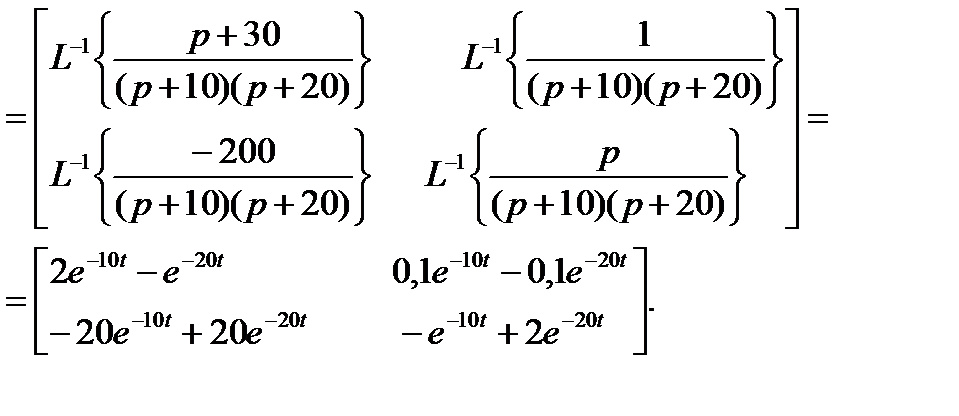Вопросы для самопроверки

1. Что такое переменные состояния? Поясните их физический смысл.

2. В чем заключается неоднозначность выбора переменных состояния?

3. Назовите основные методы выбора переменных состояния.

4. Между какими сигналами устанавливает связь матрица наблюдения?

5. Что такое характеристическая матрица?

6. От чего зависит размерность матрицы управления?

7. Запишите векторные уравнения состояния системы.

8. Назовите способы определения фундаментальной матрицы системы.