Напряжённость электростатического поля, образованного окружностью с заданной линейной плотностью электрического заряда.
Пусть окружность радиуса 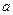 с центром в начале цилиндрической системы координат
с центром в начале цилиндрической системы координат 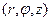 расположена в плоскости
расположена в плоскости 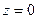 (рис.1). Элемент длины окружности
(рис.1). Элемент длины окружности 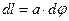 несёт элементарный заряд
несёт элементарный заряд 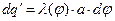 ,
, 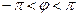 . Декартовы координаты точки наблюдения M описываются соотношениями:
. Декартовы координаты точки наблюдения M описываются соотношениями:
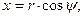
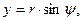
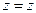 . (1)
. (1)
Декартовы координаты точки расположения элементарного электрического заряда определены зависимостями:
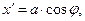
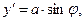
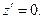 (2)
(2)
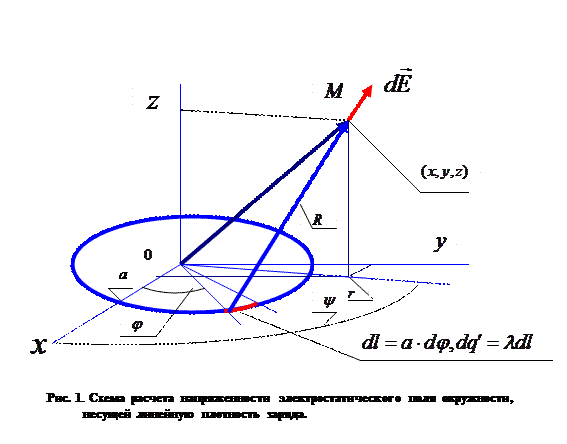 Расстояние между точкой расположения элементарного заряда и точкой наблюдения имеет вид:
Расстояние между точкой расположения элементарного заряда и точкой наблюдения имеет вид:
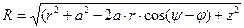 . (3)
. (3)
Дифференциалы проекций вектора напряженности электростатического поля на оси декартовой системы координат запишем в форме:
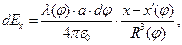
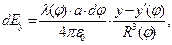
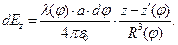 (4)
(4)
Формальное решение проблемы осуществляется с помощью следующих квадратур:
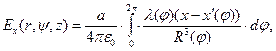 (5)
(5)
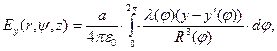 (6)
(6)
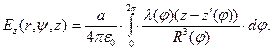 (7)
(7)
Ниже рассмотрим случай равномерного распределения электрического заряда по длине окружности ( 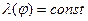 ). Выражения (5)-(7) при этом упрощаются, но, к сожалению, не настолько, чтобы вычисление квадратур стало тривиальным. Учитывая осевую симметрию распределения электрического заряда, можно воспользоваться возможностью направить ось абсцисс декартовой системы координат в точку наблюдения и считать это направление началом отсчета угловой переменной в рассматриваемых квадратурах
). Выражения (5)-(7) при этом упрощаются, но, к сожалению, не настолько, чтобы вычисление квадратур стало тривиальным. Учитывая осевую симметрию распределения электрического заряда, можно воспользоваться возможностью направить ось абсцисс декартовой системы координат в точку наблюдения и считать это направление началом отсчета угловой переменной в рассматриваемых квадратурах  . Результаты вычисления квадратур (5)-(7) можно записать с помощью специальных функций математической физики, табулированных в математических таблицах и «зашитых» в системах символьных вычислений математического обеспечения современных персональных компьютеров:
. Результаты вычисления квадратур (5)-(7) можно записать с помощью специальных функций математической физики, табулированных в математических таблицах и «зашитых» в системах символьных вычислений математического обеспечения современных персональных компьютеров:
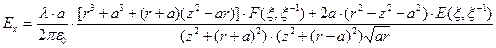 , (8)
, (8)
 (9)
(9)
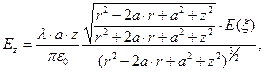 (10)
(10)
где
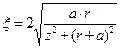 ,
, 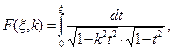
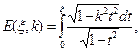
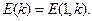 (11)
(11)
Интегралы в соотношениях (11) имеют специальные названия: неполный эллиптический интеграл первого рода, неполный эллиптический интеграл второго рода и полный эллиптический интеграл второго рода. При использовании специального математического обеспечения персональных компьютеров вычисление этих зависимостей не сложнее вычисления привычных со школы тригонометрических функций.
Если точка наблюдения расположена на оси симметрии (r = 0), а линейная плотность 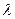 электрического заряда на рассматриваемой окружности является постоянной величиной, то единственной отличной от нуля компонентой напряженности электрического поля будет осевая компонента:
электрического заряда на рассматриваемой окружности является постоянной величиной, то единственной отличной от нуля компонентой напряженности электрического поля будет осевая компонента:
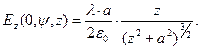 (12)
(12)
Выражение (12) получено с помощью предельного перехода 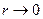 в зависимостях (8) и (10) с использованием системы символьных вычислений Maple. Этот же результат можно получить непосредственно из соотношений (5)-(7), все интегралы при этом вычисляются до конца.
в зависимостях (8) и (10) с использованием системы символьных вычислений Maple. Этот же результат можно получить непосредственно из соотношений (5)-(7), все интегралы при этом вычисляются до конца.
Легко видеть, при значениях 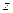 , значительно превышающих величину радиуса кольца
, значительно превышающих величину радиуса кольца 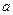 , напряженность электрического поля мало отличается от напряжённости поля, образованного суммарным точечным электрическим зарядом кольца, помещенным в начало координат.
, напряженность электрического поля мало отличается от напряжённости поля, образованного суммарным точечным электрическим зарядом кольца, помещенным в начало координат.
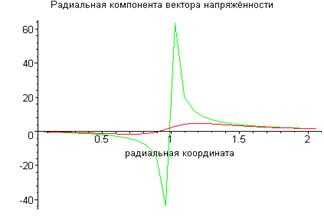
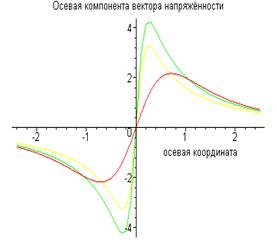
На приведённых ниже рисунках показаны результаты расчётов радиальной и осевой составляющих вектора напряжённости электрического поля (рис.2 и рис.3).
Линия «с разрывом» на первом из них построена для случая 
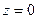 , линия без разрыва построена для случая
, линия без разрыва построена для случая 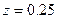 .
.
|

На рис. 2 вдоль горизонтальной оси отложена осевая координата точки наблюдения. Линии графика описывают поведение величины 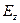 при изменении координаты
при изменении координаты 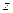 для случаев
для случаев 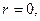
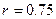 и
и 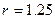 . Для убедительности примера приведем численные результаты для координаты
. Для убедительности примера приведем численные результаты для координаты 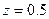 :
: 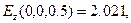
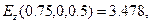
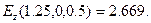 Результаты получены при
Результаты получены при 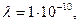
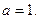 Все величины имеют размерность, соответствующую системе СИ.
Все величины имеют размерность, соответствующую системе СИ.
2.2.6.4. Напряжённость электростатического поля, образованного винтовой линией с известной погонной плотностью электрического заряда.
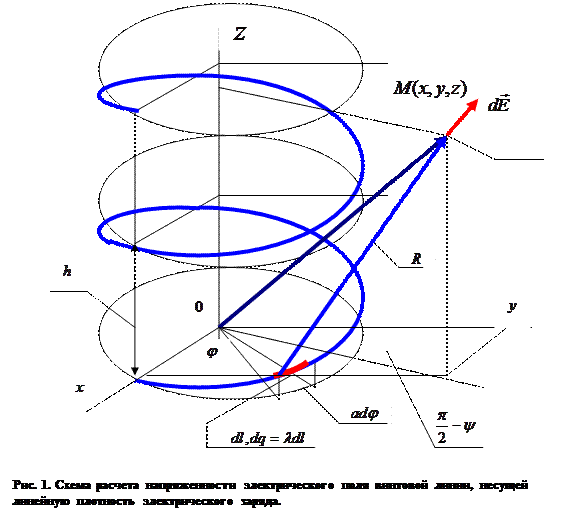
Винтовая линия является пространственной кривой, декартовы координаты точек которой удовлетворяют следующим параметрическим уравнениям:
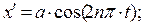
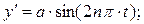
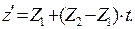 (1)
(1)
Протяженность винтовой линии вдоль оси аппликат ограничена разностью координат 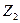 и
и 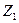 , кривая «навивается» на цилиндрическую поверхность с радиусом поперечного сечения
, кривая «навивается» на цилиндрическую поверхность с радиусом поперечного сечения 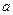 , образуя «правый винт». Шаг винтовой линии составляет величину
, образуя «правый винт». Шаг винтовой линии составляет величину 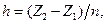 значение
значение 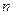 не обязательно целое (Рис.1). Погонная (линейная) плотность электрического заряда задана как известная функция параметра
не обязательно целое (Рис.1). Погонная (линейная) плотность электрического заряда задана как известная функция параметра 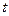 :
: 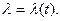 Представляет интерес определение компонент вектора напряженности электрического поля, образованного рассматриваемым распределением электрического заряда в точке наблюдения М(x,y,z).
Представляет интерес определение компонент вектора напряженности электрического поля, образованного рассматриваемым распределением электрического заряда в точке наблюдения М(x,y,z).
Параметрические уравнения винтовой линии (1) позволяют определить длину элементарного отрезка кривой, который содержит элементарный электрический заряд 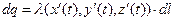 :
:
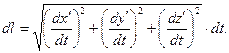 (2)
(2)
Далее используем известную методику получения результата:
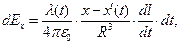
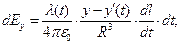
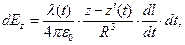 (3)
(3)
где величина R определена соотношением: 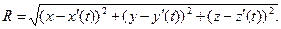
Вычисление компонент вектора напряженности электрического поля сводится к вычислению квадратур:
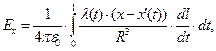
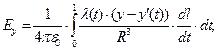 (4)
(4)
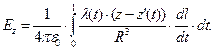
Даже для случая равномерного распределения электрического заряда по длине винтовой линии для вычисления интегралов в выражениях (4) приходится использовать численные методы. В качестве примера используем значения 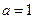 м,
м, 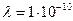 Кл/м,
Кл/м, 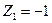 м.,
м., 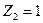 м.,
м., 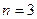 и рассчитаем значения проекций вектора напряженности электрического поля для некоторых характерных точек пространства. Так, для точки с координатами (5,0,0) получаем вектор напряженности с проекциями (0.687,0,0), для точки с координатами (5,5,0) - вектор (0.242,0.242,0.002), для точки с координатами (5,5,5) - вектор (0.130,0.131,0.131). На приведённом ниже рисунке показано изменение вдоль оси z величины осевой составляющей напряжённости электрического поля на оси винтовой линии для тех же параметров распределения электрического заряда. Все физические величины, использованные в расчёте, имеют размерность системы СИ.
и рассчитаем значения проекций вектора напряженности электрического поля для некоторых характерных точек пространства. Так, для точки с координатами (5,0,0) получаем вектор напряженности с проекциями (0.687,0,0), для точки с координатами (5,5,0) - вектор (0.242,0.242,0.002), для точки с координатами (5,5,5) - вектор (0.130,0.131,0.131). На приведённом ниже рисунке показано изменение вдоль оси z величины осевой составляющей напряжённости электрического поля на оси винтовой линии для тех же параметров распределения электрического заряда. Все физические величины, использованные в расчёте, имеют размерность системы СИ.
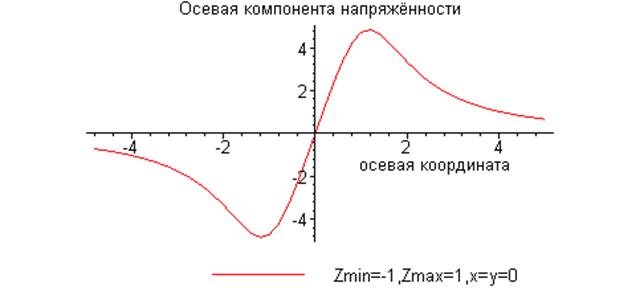

При анализе графика, приведенного на рисунке 2, интересно отметить, что напряженность электрического поля в начале координат обращается в нуль, растет с увеличением координаты z до определённого значения, а потом убывает с увеличением расстояния от винтовой линии. Характер показанной зависимости определяется относительной мерой влияния ориентации в пространстве элементарных векторных слагаемых и уменьшением последних с увеличением расстояния от элементарного заряда до точки наблюдения. На первом участке имеем «сильное поле навстречу друг другу», а на втором – «слабое поле однонаправленных слагаемых».
Дата добавления: 2017-09-01; просмотров: 2090;











