Способы представления скалярного и векторного полей.

Строгое и полное абстрактное определение скалярного или векторного поля требует некоторого умственного напряжения для осознания сущности рассматриваемого объекта. Физики и математики потратили немало усилий, чтобы представление о поле физической величины сделать более наглядным, значит, и более понятным. С некоторыми из этих представлений познакомимся ниже.

Скалярное поле описывает зависимость скалярной величины от пространственных координат точки наблюдения. В одномерном случае достаточно полное представление о скалярной величине даёт график функции 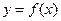. В случае двух пространственных координат можно воспользоваться либо пространственным графиком 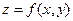- такой геометрический образ можно себе представить, либо семейством линий 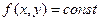- линий постоянного уровня. Примером подобного приёма является изображение холма на географической карте. В случае трёх пространственных переменных можно вообразить только семейство поверхностей уровня 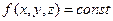, или пытаться построить некоторую последовательность «сечений» объекта: сечения плоскостью 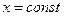, например. Но восприятие подобной информации не менее затруднено, чем абстрактное представление.

Представление векторного поля затруднено уже тем, что структура векторной величины сложнее структуры скалярной величины. Если представлять себе векторную величину как стрелку, длина которой равна модулю векторной величины, а направление стрелки в пространстве совпадает с ориентацией векторной величины в пространстве, можно попытаться для некоторого конечного множества точек пространства нарисовать в определенном масштабе векторные величины рассматриваемого поля. Подобное построение в принципе выполнимо, вопрос только в том, насколько информативным будет изображение.

Качественный характер закономерностей векторного поля часто отражают с помощью так называемых «силовых» или «векторных» линий.

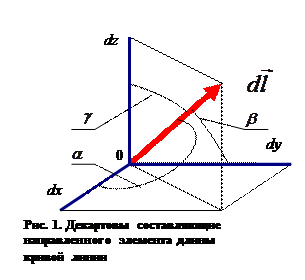
Рассмотрим подробнее эту возможность. Силовую линию определим как пространственную линию, касательная к которой в каждой точке линии совпадает по направлению с векторной величиной, поле которой мы описываем, в той же точке пространства. Иначе, направленный элемент длины силовой линии параллелен векторной величине в одной и той же точке пространства. Условие параллельности двух векторов можно записать в двух эквивалентных формах:

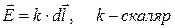(1)

или с использованием операции векторного произведения

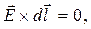(2)

что в координатной форме записи приводит к системе дифференциальных уравнений

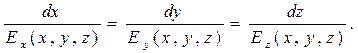(3)

здесь 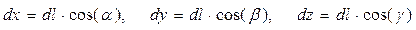, элементарная длина 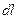отрезка пространственной кривой умножается на направляющие косинусы в системе декартовой системы координат. Уравнения (3) - дифференциальные уравнения силовой линии. Зависимост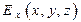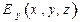и , и 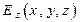могут оказаться достаточно сложными, поэтому аналитически проинтегрировать систему (3) в общем случае не удается. Численные методы обладают значительно более широкими возможностями. Действительно, пусть точка 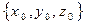принадлежит силовой линии, в этой точке известны 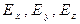, причем (для определенности) 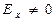. Если задаться такой величиной смещения вдоль силовой линии, что координата x₀ получит приращение dx, то для дифференциалов координат dy и dz получаем:

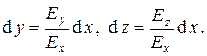(4)

Но тем самым мы определили точку 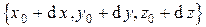, которая тоже принадлежит силовой линии. Повторяя этот процесс, можно последовательно получить координаты силовой линии, проходящей через начальную точку .

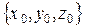Ниже показаны некоторые типичные изображения силовых линий системы (для простоты) из двух электрических зарядов (рис.3 - 5).

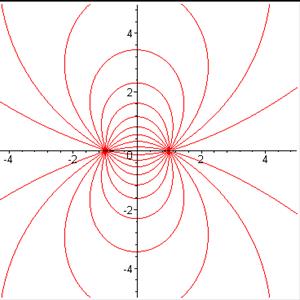
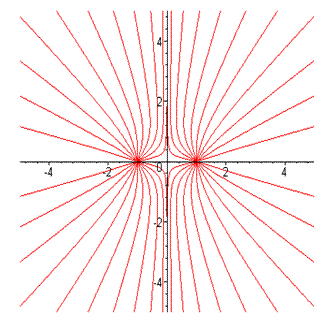
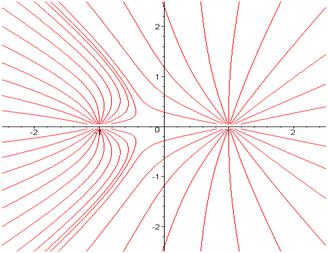
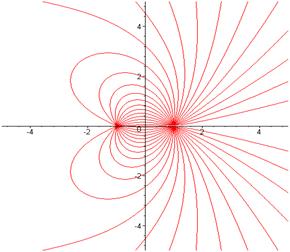
На приведённых рисунках следует обратить внимание на симметрию расположения силовых линий напряженности электрического поля, образованного двумя одинаковыми по величине электрическими зарядами. На приведенных рисунках не показано стрелками положительное направление вдоль силовых линий.

Пользуясь понятием “силовая линия векторного поля”, следует иметь в виду следующие обстоятельства:

- cиловых линий существует бесконечное множество;

- cиловая линия сама по себе не содержит информации о величине вектора;

- силовая линия сама по себе не определяет полностью направление вектора (при выбранном положительном направлении вдоль силовой линии вектор может быть направлен как в положительном направлении, так и в противоположном);

- попытки отразить локальную величину векторного поля густотой проводимых силовых линий небезупречны с точки зрения строгости рассмотрения: конечное число проводимых силовых линий не обеспечивает точности представления поля и может порождать иллюзию возникновения несуществующих в действительности источников векторного поля.

В силу сказанного описание векторного поля с помощью силовых линий не может быть полным, однако, графическое представление совокупности отдельных силовых линий, их поведение в пространстве могут служить вспомогательным средством глубже понять свойства изучаемого векторного поля. Полное представление о скалярном или векторном поле по мнению нобелевского лауреата по физике Р. Фейнмана содержится в их абстрактном определении, это тем более важно для уяснения его физического содержания (физического смысла).