Напряжённость электростатического поля, образованного заряженным отрезком прямой линии.
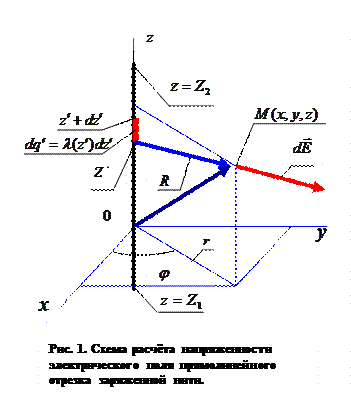
При расчёте напряжённости электростатического поля, образованного отрезком прямой линии с заданной погонной плотностью 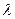 электрического заряда, следует обратить внимание на то, чтораспределение электрических зарядов в пространстве обладает свойством осевой симметрии. При этом осью симметрии является рассматриваемая прямая линия (Рис.1). В цилиндрической системе координат
электрического заряда, следует обратить внимание на то, чтораспределение электрических зарядов в пространстве обладает свойством осевой симметрии. При этом осью симметрии является рассматриваемая прямая линия (Рис.1). В цилиндрической системе координат 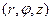 ось
ось 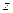 направим вдоль оси симметрии, начало системы координат выберем произвольно. Допустим, что известна зависимость
направим вдоль оси симметрии, начало системы координат выберем произвольно. Допустим, что известна зависимость 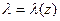 , где координата z изменяется в пределах
, где координата z изменяется в пределах 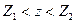 , Z1 и Z2 - координаты начала и конца рассматриваемого отрезка. Декартовы координаты точки наблюдения М определим соотношениями:
, Z1 и Z2 - координаты начала и конца рассматриваемого отрезка. Декартовы координаты точки наблюдения М определим соотношениями:
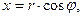
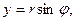
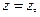 (1)
(1)
а координаты точки расположения элементарного заряда 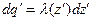 соответственно:
соответственно:
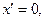
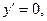
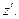 (2)
(2)
 В силу осевой симметрии рассматриваемой задачи ниже полагаем
В силу осевой симметрии рассматриваемой задачи ниже полагаем 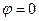 , при этом выполняется условие
, при этом выполняется условие 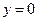 . Расстояние от точки расположения элементарного заряда
. Расстояние от точки расположения элементарного заряда 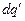 до точки наблюдения М равно:
до точки наблюдения М равно:
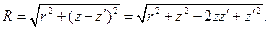 (3)
(3)
Выпишем проекции дифференциалов вектора напряжённости электростатического поля на оси декартовой системы координат в точке наблюдения:
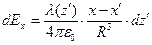 ,
, 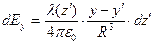 , (4)
, (4) 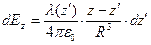 .
.
Выполним интегрирование по переменной 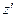 в пределах от
в пределах от 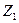 до
до 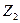 :
:
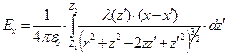 ,
, 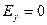 ,
, 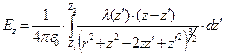 . (5)
. (5)
Квадратуры в соотношениях (5) можно вычислить аналитически или численно для конкретных зависимостей 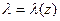 и заданных координат точки наблюдения. Ниже получим результаты для простейшего равномерного распределения (
и заданных координат точки наблюдения. Ниже получим результаты для простейшего равномерного распределения ( 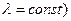 электрического заряда по длине отрезка [Z1,Z2]:
электрического заряда по длине отрезка [Z1,Z2]:
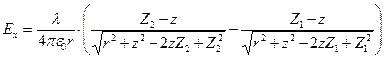 , (6)
, (6)
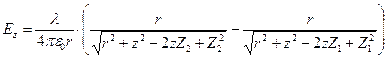 . (7)
. (7)
Заметим, что выражение (6) описывает радиальную составляющую вектора напряженности электрического поля, поскольку в выкладках использована специальным образом ориентированная система координат. При произвольном значении угловой координаты точки наблюдения 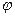 , естественно, можно получить:
, естественно, можно получить:
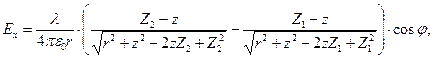 (8)
(8)
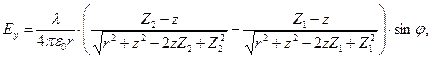 (9)
(9)
выражение (7) остаётся при этом без изменений.
Если точка наблюдения лежит в плоскости 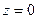 , результаты упрощаются:
, результаты упрощаются:
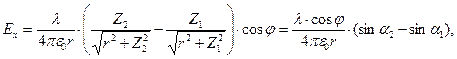 (10)
(10)
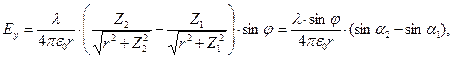 (11)
(11)
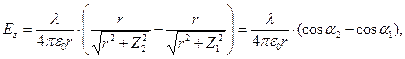 (12)
(12)
где углы 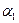 и
и 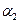 определены соотношениями:
определены соотношениями:
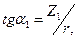
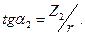 (13)
(13)
Легко видеть, что для бесконечной прямой с равномерным распределением электрического заряда по длине 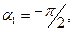
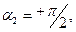 в итоге получаем соотношения:
в итоге получаем соотношения:
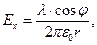
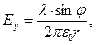
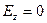 . (14)
. (14)
Модуль вектора напряженности электрического поля в точке наблюдения при этом выражается зависимостью:
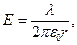 (15)
(15)
его величина совпадает с радиальной компонентой вектора напряженности. В одном из последующих разделов курса этот результат будет получен с помощью теоремы Гаусса для вектора напряженности электростатического поля.
Дата добавления: 2017-09-01; просмотров: 2034;











