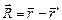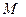Напряжённость электростатического поля, образованного плоским прямоугольником с известной поверхностной плотностью электрического заряда.
|

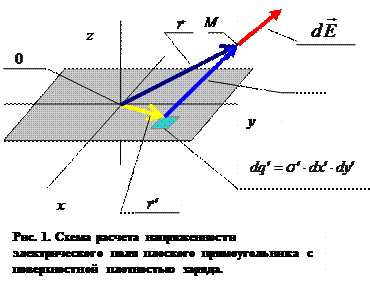 Пусть плоский прямоугольник с известной поверхностной плотностью электрического заряда расположен в плоскости
Пусть плоский прямоугольник с известной поверхностной плотностью электрического заряда расположен в плоскости 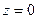 декартовой системы координат, а его стороны ориентированы параллельно осям
декартовой системы координат, а его стороны ориентированы параллельно осям 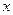 и
и 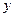 соответственно, центр симметрии прямоугольника совпадает с началом координат. Площадь прямоугольника определяется выражением
соответственно, центр симметрии прямоугольника совпадает с началом координат. Площадь прямоугольника определяется выражением 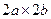 , элементарный электрический заряд описывается выражением
, элементарный электрический заряд описывается выражением 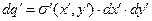 . Координаты точки наблюдения М(х,y,z) произвольны. Подлежит расчёту напряженность электростатического поля в произвольной точке М(x,y,z).
. Координаты точки наблюдения М(х,y,z) произвольны. Подлежит расчёту напряженность электростатического поля в произвольной точке М(x,y,z).
Координаты точки расположения бесконечно малого электрического заряда имеют вид 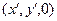 . Вычислим дифференциалы компонент вектора напряженности электрического поля в окрестности точки наблюдения:
. Вычислим дифференциалы компонент вектора напряженности электрического поля в окрестности точки наблюдения:
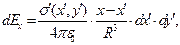
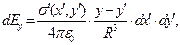
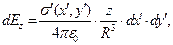 (1)
(1)
где
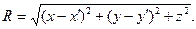 (2)
(2)
Значения компонент вектора напряженности электрического поля в произвольной точке наблюдения получаются формальным интегрированием выражений (1) по площади заряженного прямоугольника. Если поверхностная плотность электрического заряда является постоянной величиной 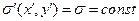 (равномерное распределение электрического заряда по площади прямоугольника), то имеют место следующие аналитические зависимости:
(равномерное распределение электрического заряда по площади прямоугольника), то имеют место следующие аналитические зависимости:
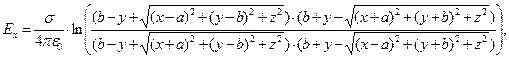 (3)
(3)
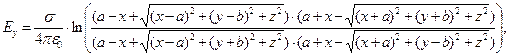 (4)
(4)
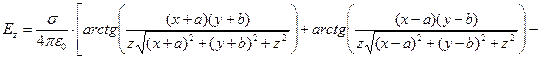
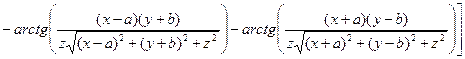 . (5)
. (5)
Примеры зависимости величин компонент вектора напряжённости электрического поля при заданном равномерном распределении заряда по площади прямоугольника от координат точки наблюдения показаны на приведённых ниже рисунках (все физические величины выражены в единицах СИ).
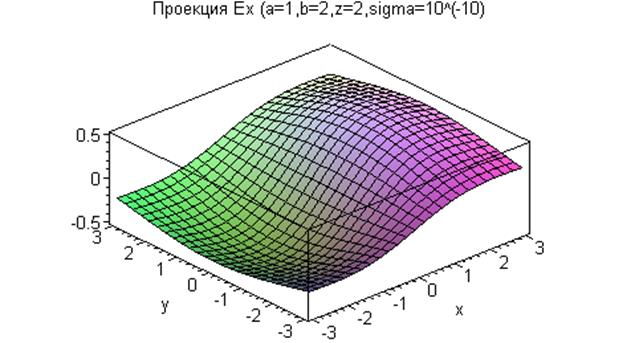

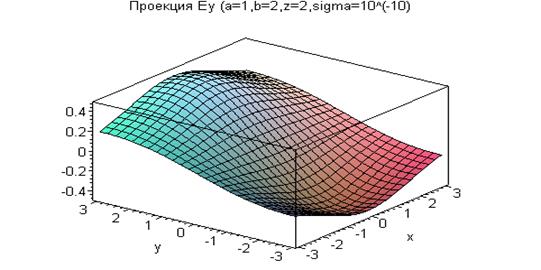

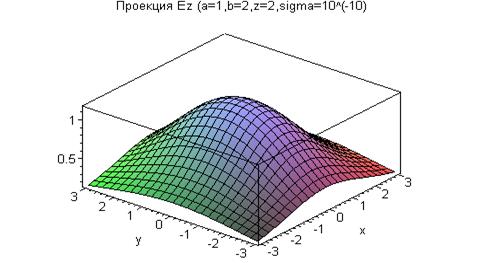

Интересно и важно отметить, что при стремлении координаты 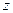 к нулю сверху от заряжённого прямоугольника и снизу, если при этом координаты х и у точки наблюдения не выходят за границы прямоугольника, касательные компоненты напряженности электрического поля равны между собой, а разность нормальных к плоскости прямоугольника компонент напряженности электрического поля, умноженная на электрическую постоянную, стремится к величине поверхностной плотности электрического заряда на поверхности.
к нулю сверху от заряжённого прямоугольника и снизу, если при этом координаты х и у точки наблюдения не выходят за границы прямоугольника, касательные компоненты напряженности электрического поля равны между собой, а разность нормальных к плоскости прямоугольника компонент напряженности электрического поля, умноженная на электрическую постоянную, стремится к величине поверхностной плотности электрического заряда на поверхности.
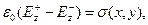 (-a<х<a,-b<у<b). (6)
(-a<х<a,-b<у<b). (6)
Это свойство электрического поля будет строго доказано в последующих разделах учебного пособия.
2.2.6.6.Напряжённость электростатического поля, образованного плоским кругом с известной поверхностной плотностью электрического заряда.
Электростатическое поле, образованное рассматриваемой конфигурацией электрического заряда (Рис.1), можно рассчитать с использованием цилиндрической системы координат
|
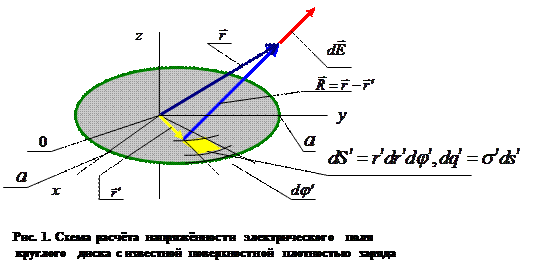
для описания распределения заряда по площади круга и декартовой системы координат для описания положения точки наблюдения. Удобно совместить начала коодинат этих систем, считая, что ось симметрии круга принята за плоскость 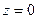 в обеих системах координат, ось
в обеих системах координат, ось 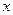 служит началом отсчёта угловой переменной в цилиндрической системе координат, а ось
служит началом отсчёта угловой переменной в цилиндрической системе координат, а ось 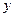 направлена так, чтобы декартова система координат была «правой». Пусть радиус круга равен
направлена так, чтобы декартова система координат была «правой». Пусть радиус круга равен 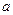 , физически бесконечно малый электрический заряд описан соотношением
, физически бесконечно малый электрический заряд описан соотношением
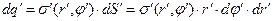 , (1)
, (1)
а координаты точки произвольной точки наблюдения М обозначены как (x,y,z). Дифференциалы проекций на оси декартовой системы координат вектора напряжённости электрического поля, образованного элементарным электрическим зарядом на поверхности круга, в точке наблюдения имеют вид:
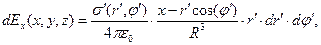 (2)
(2) 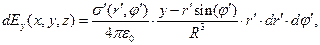 (3)
(3)
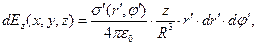 (4)
(4)
где 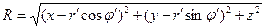 - расстояние от точки расположения элементарного заряда до точки наблюдения.
- расстояние от точки расположения элементарного заряда до точки наблюдения.
Проекции вектора напряжённости электрического поля на оси декартовой системы координат в точке наблюдения можно получить интегрированием соотношений (2)-(4) по площади круга. К сожалению, этот вариант расчёта не приводит к удобным математическим зависимостям, даже если принять поверхностную плотность электрического заряда постоянной величиной. Численные значения составляющих вектора напряжённости для фиксированной точки наблюдения получаются достаточно просто с использованием специального математического обеспечения современных компьютеров.
В частном случае равномерного распределения электрического заряда по площади круга 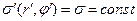 и при условии, что точка наблюдения расположена на оси симметрии системы, аналитические выкладки проводятся до конца и приводят к следующим результатам:
и при условии, что точка наблюдения расположена на оси симметрии системы, аналитические выкладки проводятся до конца и приводят к следующим результатам:
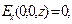
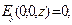
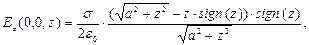
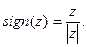 (5)
(5)
На рисунке 2 показана зависимость осевой составляющей напряженности электрического поля на оси симметрии системы в зависимости от осевой координаты. Расчёты выполнены для случая 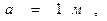
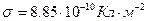 , значения осевой координаты имеют размерность
, значения осевой координаты имеют размерность 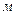 . Обращает на себя внимание разрыв значений напряженности электрического поля при переходе через заряженную поверхность круга. Из результата (5) следует:
. Обращает на себя внимание разрыв значений напряженности электрического поля при переходе через заряженную поверхность круга. Из результата (5) следует:
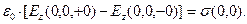 (6)
(6)
|
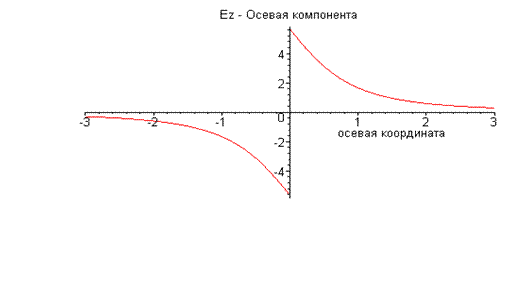
Соотношение, аналогичное соотношению (6), имело место при рассмотрении электрического поля в окрестности заряженного плоского прямоугольника. Это обстоятельство позволяет надеяться, что величина скачка нормальной компоненты напряженности при переходе через заряженную поверхность определяется локальными факторами и не зависит от геометрии контура пластины в плане.
На большом удалении от плоскости круга электрическое поле описывается зависимостью, аналогичной зависимости напряженности электрического поля, образованного суммарным «точечным» зарядом системы, сосредоточенным в центре круга.
2.2.6.7. Напряжённость электростатического поля, образованного сферой с известной поверхностной плотностью электрического заряда.
Пусть сфера радиуса 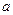 заряжена электрическим зарядом таким образом, что заряд элемента её поверхности можно описать соотношением:
заряжена электрическим зарядом таким образом, что заряд элемента её поверхности можно описать соотношением:
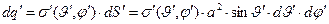 , (1)
, (1)
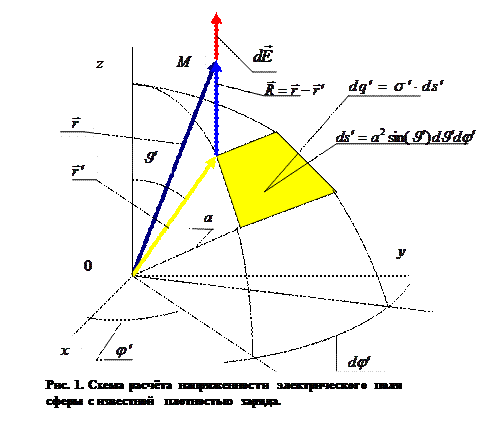
где 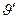 и
и 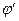 - угловые переменные сферической системы координат, начало которой совпадает с центром сферы (Рис. 1). Дифференциалы проекций вектора напряжённости электростатического поля в точке наблюдения М на оси соответствующей системы декартовых координат (ось х соответствует направлению
- угловые переменные сферической системы координат, начало которой совпадает с центром сферы (Рис. 1). Дифференциалы проекций вектора напряжённости электростатического поля в точке наблюдения М на оси соответствующей системы декартовых координат (ось х соответствует направлению 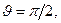
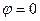 ) имеют вид:
) имеют вид:
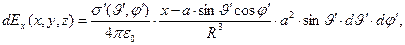 (2)
(2)
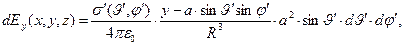 (3)
(3)
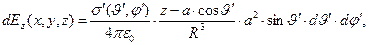 (4)
(4)
где расстояние между точкой расположения элементарного заряда и точкой наблюдения опрделено выражением:
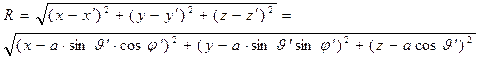 . (5)
. (5)
 В общем случае при произвольной зависимости поверхностной плотности заряда от координат точки расположения элементарного заряда на поверхности сферы можно записать квадратуры для величин
В общем случае при произвольной зависимости поверхностной плотности заряда от координат точки расположения элементарного заряда на поверхности сферы можно записать квадратуры для величин 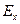 ,
, 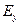 и
и 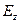 , для вычисления которых можно использовать приёмы численного интегрирования.
, для вычисления которых можно использовать приёмы численного интегрирования.
В частном случае равномерного распределния заряда по поверхности сферы, пользуясь симметрией распределения заряда, сферическую систему координат можно выбрать так, чтобы направление 
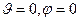 совпадало бы с направлением на точку наблюдения. В этом случае x=0, y=0 и интегрирование по угловой переменной
совпадало бы с направлением на точку наблюдения. В этом случае x=0, y=0 и интегрирование по угловой переменной 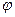 для компонент напряженности
для компонент напряженности 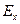 и
и 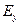 даёт в результате нуль, а для компоненты
даёт в результате нуль, а для компоненты 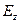 сводится к простому умножению подынтегральной функции на
сводится к простому умножению подынтегральной функции на 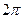 :
:
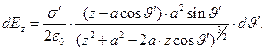 (6)
(6)
Интегрирование по переменной 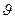 в пределах от 0 до
в пределах от 0 до 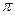 приводит к результату:
приводит к результату:
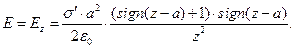 (7)
(7)
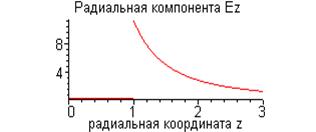
 Зависимость (7) (см. рис. 2) фактически описывает изменение «радиальной» компоненты вектора напряженности в системе декартовых координат, специально ориентированной относительно точки наблюдения, в которой координата
Зависимость (7) (см. рис. 2) фактически описывает изменение «радиальной» компоненты вектора напряженности в системе декартовых координат, специально ориентированной относительно точки наблюдения, в которой координата 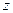 играет роль расстояния от центра сферы до точки наблюдения. Заметим, что эта величина является нормальной по отношению к поверхности сферы компонентой напряженности электрического поля. При
играет роль расстояния от центра сферы до точки наблюдения. Заметим, что эта величина является нормальной по отношению к поверхности сферы компонентой напряженности электрического поля. При 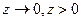 из зависимости (7) следует
из зависимости (7) следует
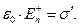 (8)
(8)
При 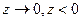 из зависимости (7) следует
из зависимости (7) следует
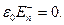 (9)
(9)
Таким образом, снова получено соотношение для скачка нормальной компоненты электрического поля при переходе через заряженную поверхность, но теперь эта поверхность не является плоской. Это укрепляет нашу уверенность в том, что обсуждаемая величина скачка зависит только от локальных параметров заряженной поверхности.
Зависимости (7) и (8) не являются тривиальными результатами. Оказывается, также как и в теории тяготения И. Ньютона, равномерное распределение источника поля по поверхности замкнутой сферы не создаёт силы внутри сферы.
В заключение приведём выражения для компонент вектора напряжённости электростатического поля, образованного электрическим зарядом, равномерно распределенным по поверхности сферы, для произвольной точки наблюдения вне заряженной сферы:
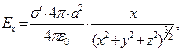
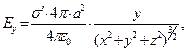
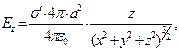 (10)
(10)
в которых без труда можно узнать зависимости для напряженности электрического поля, образованного «точечным» суммарным зарядом системы, расположенным в центре сферы.
Дата добавления: 2017-09-01; просмотров: 2890;