Напряжённость электростатического поля, образованного шаром с известной объёмной плотностью электрического заряда.
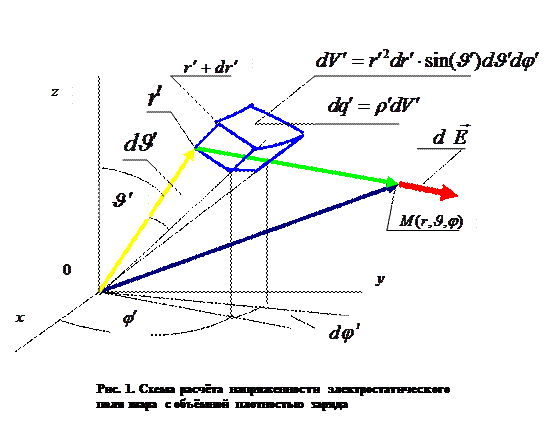
Рассмотрим шар радиуса 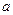 , центр которого расположен в начале декартовой системы координат Oxyz (Рис.1). Координаты точки наблюдения внутри и вне шара обозначим не штрихованными переменными, а координаты элементарного объёма шара – штрихованными переменными. Учитывая геометрию рассматриваемого тела, введём сферическую систему координат
, центр которого расположен в начале декартовой системы координат Oxyz (Рис.1). Координаты точки наблюдения внутри и вне шара обозначим не штрихованными переменными, а координаты элементарного объёма шара – штрихованными переменными. Учитывая геометрию рассматриваемого тела, введём сферическую систему координат
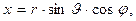
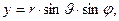
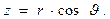 (1)
(1)
Допустим, что внутри шара отлична от нуля объёмная плотность электрического заряда 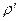 , так что элемент объёма шара содержит электрический заряд величины
, так что элемент объёма шара содержит электрический заряд величины
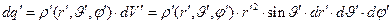 . (2)
. (2)
Дифференцциалы проекций вектора напряжённости электростатического поля на оси декартовой системы в сферических переменных имеют вид:
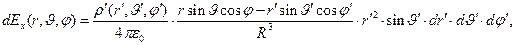 (3)
(3)
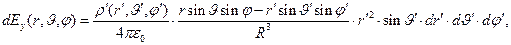 (4)
(4)
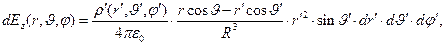 (5)
(5)
где расстояние между точкой расположения элементарного заряда и точкой наблюдения определено зависимостями:
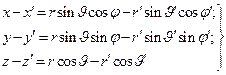 (6)
(6)
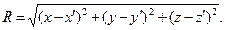 (7)
(7)
В общем случае для вычисления проекций вектора напряжённости электрического поля необходимо трижды проинтегрировать выражения (3)-(5): по угловой координате 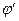 в пределах от 0 до
в пределах от 0 до 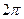 , по угловой переменной
, по угловой переменной 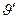 в пределах от 0 до
в пределах от 0 до 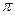 и по радиальной переменной
и по радиальной переменной 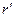 в пределах от 0 до
в пределах от 0 до 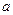 . Для фиксированного положения точки наблюдения величины проекций вектора
. Для фиксированного положения точки наблюдения величины проекций вектора 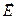 можно вычислить, используя специальное математическое обеспечение современных персональных компьютеров.
можно вычислить, используя специальное математическое обеспечение современных персональных компьютеров.
Для частного случая равномерного распределения электрического заряда по объёму шара с учетом симметрии задачи удобно считать, что точка наблюдения лежит на направлении 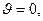 т.е. это направление принято за «главную» ось симметрии. В этом случае, оказывается, величина
т.е. это направление принято за «главную» ось симметрии. В этом случае, оказывается, величина 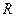 не зависит от угловой переменной
не зависит от угловой переменной 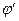 , интегрирование по этой переменной позволяет получить соотношения:
, интегрирование по этой переменной позволяет получить соотношения:
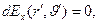
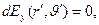
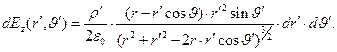 (8)
(8)
Из соотношений (8) следует, что единственной отличной от нуля компонентой вектора напряженности является «радиальная» компонента 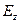 . Проинтегрируем зависимость (8) по оставшейся угловой координате:
. Проинтегрируем зависимость (8) по оставшейся угловой координате:
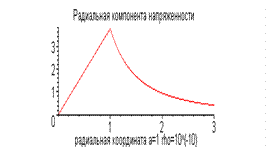
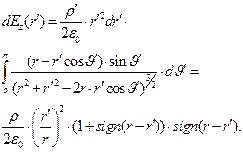 (9)
(9)
 Легко видеть
Легко видеть 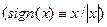 , что при
, что при 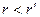 выражение (9) обращается в нуль, это является подтверждением результата, полученного при рассмотрении электростатического поля, образованного равномерно заряженной сферой. В рассматриваемом случае выражение (9) описывает электростатическое поле, образованное равномерно заряженным тонким шаровым слоем. При последующем интегрировании зависимости (9) следует учитывать, что переменная интегрирования не должна быть больше радиальной координаты точки наблюдения, если точка наблюдения находится вутри шара. Если точка наблюдения находится вне шара, интегрирование проводим в пределах от нуля до радиуса граничной поверхности а. Таким образом, при интегрировании зависимости (9) получаем
выражение (9) обращается в нуль, это является подтверждением результата, полученного при рассмотрении электростатического поля, образованного равномерно заряженной сферой. В рассматриваемом случае выражение (9) описывает электростатическое поле, образованное равномерно заряженным тонким шаровым слоем. При последующем интегрировании зависимости (9) следует учитывать, что переменная интегрирования не должна быть больше радиальной координаты точки наблюдения, если точка наблюдения находится вутри шара. Если точка наблюдения находится вне шара, интегрирование проводим в пределах от нуля до радиуса граничной поверхности а. Таким образом, при интегрировании зависимости (9) получаем
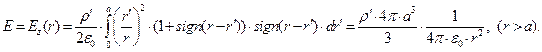 (10)
(10)
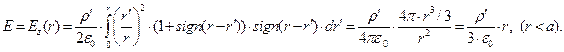 (11)
(11)
Форма записи зависимостей (10) и (11) позволяет обнаружить, что при выполнении условия 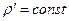 алгебраическая величина напряжённости электростатического поля в рассматриваемой точке пространства определяется величиной суммарного электрического заряда, находящегося в объёме шара радиуса
алгебраическая величина напряжённости электростатического поля в рассматриваемой точке пространства определяется величиной суммарного электрического заряда, находящегося в объёме шара радиуса 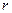 , делённой на площадь поверхности сферы того же радиуса и делённой на величину электрической постоянной
, делённой на площадь поверхности сферы того же радиуса и делённой на величину электрической постоянной 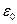 . Для случая
. Для случая 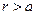 приведённый результат остаётся в силе, только, естественно, величину электрического заряда надо рассчитать по объёму шара радиуса
приведённый результат остаётся в силе, только, естественно, величину электрического заряда надо рассчитать по объёму шара радиуса 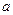 . Полученный результат находится в полном согласии с теоремой Гаусса для напряжённости электростатического поля. Теорема Гаусса обсуждается в следующем разделе пособия.
. Полученный результат находится в полном согласии с теоремой Гаусса для напряжённости электростатического поля. Теорема Гаусса обсуждается в следующем разделе пособия.
Графическое представление зависимостей (10) и (11) приведено на рис. 2. Важно отметить, что в отсутствие поверхностной плотности электрического заряда нормальная к граничной поверхности шара компонента напряженности электрического поля не испытывает разрыва, а остаётся непрерывной функцией радиальной координаты.
В заключение приведём выражения для составляющих вектора напряжённости электрического поля, образованного равномерным распределением заряда по объёму шара для произвольного положения точки наблюдения:
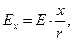
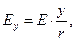
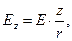 (12)
(12)
где величина Е определена либо зависимостью (10), либо зависимостью (11).
Дата добавления: 2017-09-01; просмотров: 1424;











