Бесконечный круглый проводящий цилиндр в поле равномерно заряженной прямолинейной нити, параллельной оси цилиндра.

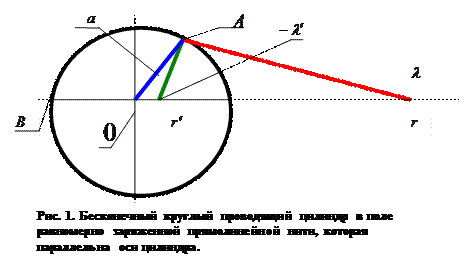Пусть ось бесконечного изначально незаряженного цилиндра с поперечным сечением в форме окружности радиуса а совпадает с продольной осью цилиндрической системы координат. Пусть параллельно оси цилиндра на расстоянии 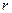от неё (Рис.1) расположена прямолинейная нить с линейной плотностью электрического заряда 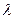. Боковая поверхность цилиндра является проводящей поверхностью. Определим параметры электростатического поля вне проводящего цилиндра. Эту задачу можно решить с помощью метода изображений. Решение рассматриваемой задачи облегчается тем, что имеет место теорема: в электростатическом поле двух бесконечных параллельных заряженных нитей с равными по величине и обратными по знаку постоянными линейными плотностями заряда найдётся эквипотенциальная цилиндрическая поверхность, ось симметрии которой параллельна описанным нитям. Покажем, что это утверждение справедливо. Пусть вторая нить расположена на расстоянии 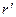от начала координат, она параллельна продольной оси и лежит в одной плоскости с первой нитью и продольной осью системы координат, заряд второй нити на единице длины по условию равен 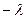. Для равномерно заряженной уединённой нити, в частности, справедливы соотношения

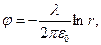
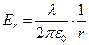, (1)

где 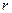- расстояние от нити до точки наблюдения (зависимость для 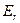может быть получена с помощью теоремы Гаусса, а зависимость для потенциала 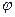следует из его определения).

При использовании цилиндрической системы координат расстояние между двумя точками пространства можно рассчитать аналогично тому, как это выполнено в предыдущем разделе при использовании сферической системы координат.

Если точка наблюдения 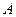принадлежит цилиндрической поверхности (рис.1), имеем

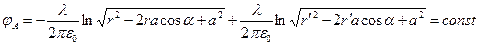. (2)

Выполнение этого условия возможно, если принять соотношение

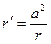. (3)

Действительно, если подставим это соотношение в предыдущую формулу, получим

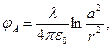(4)

т.е. величину, которая не зависит от угловой координаты 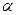и в силу этого является постоянной на цилиндрической поверхности.

Для произвольной точки пространства М вне проводящей цилиндрической поверхности (рис.2) можно записать выражение для потенциала и напряженности поля в цилиндрической системе координат:

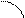
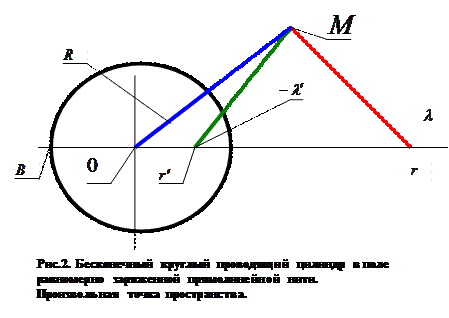
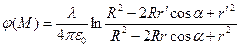, (5)

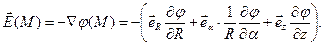(6)

Радиальная компонента напряжённости электростатического поля имеет вид:

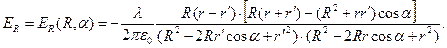(7)

Полученный результат позволяет вычислить распределение поверхностной плотности индуцированного электрического заряда на боковой поверхности цилиндра:

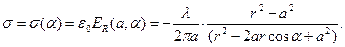(8)

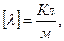
Проверим физическую размерность результата: 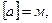следовательно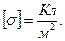

Интересно вычислить суммарный индуцированный электрический заряд на единице длины боковой поверхности цилиндра. Проинтегрируем выражение для поверхностной плотности индуцированного заряда на цилиндрической поверхности

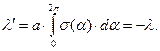(9)

На поверхности проводящего цилиндра образовался индуцированный заряд, величина погонной плотности которого совпадает с величиной погонной плотности заряда нити, а знак индуцированного заряда противоположен знаку заряда нити.

Индуцированный электрический заряд неравномерно распределён по поверхности проводящего цилиндра. Степень отмеченной неравномерности можно оценить по графикам рис. 3, на которых вдоль радиальных направлений отложены величины

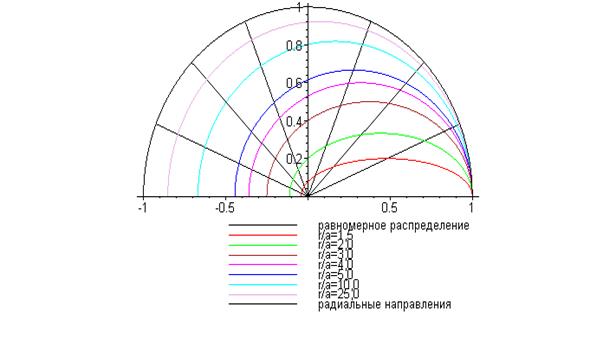
отношения локальной поверхностной плотности индуцированного электрического заряда к максимальной поверхностной плотности заряда 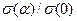. Легко видеть, что с увеличением расстояния нити от оси проводящего цилиндра распределение поверхностной плотности заряда становится более равномерным. В этом семейство индикатрис распределения индуцированного заряда на проводящем цилиндре похоже на семейство индикатрис распределения индуцированного заряда на проводящей сфере (рис. 3 предыдущего раздела), хотя количественное различие имеет место. Качественное различие результатов состоит в том, что величина погонной плотности индуцированного заряда (9) в рассматриваемом случае не зависит от расстояния заряженной нити от оси цилиндрической поверхности.

Рассмотрим угловую составляющую напряжённости электростатического поля в произвольной точке пространства:

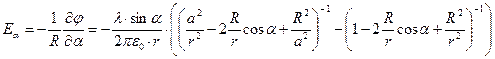. (10)

Из этого соотношения следуют два принципиальных результата. Первый из них состоит в том, что на поверхности проводящего цилиндра величина 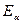должна обращаться в нуль. Легко проверить, что это условие действительно выполняется при подстановке 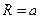. Второй результат состоит в том, что электростатическое поле должно быть потенциальным, циркуляция вектора напряжённости по произвольному замкнутому контуру должна равняться нулю. Рассмотрим контур 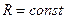. С помощью пакета символьных вычислений Maple получаем

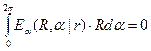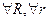, . (11)

Для частного типа замкнутых контуров условие потенциальности действительно выполняется, но при этом остаётся сомнение, будет ли условие потенциальности выполнено для произвольного контура. Это сомнение можно разрешить, если вычислить компоненты вектора 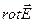для произвольной точки пространства и убедиться, что все они обращаются в нуль. А если вспомнить, что 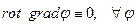, то проверку в рассматриваемом случае можно сделать только для того, чтобы убедиться в правильности полученных результатов.