Напряженность электростатического поля вдали от системы электрических зарядов конечных размеров.

Рассмотрим специфику распределения напряженности электростатического поля на расстояниях, значительно превышающих характерный размер области, в которой содержится электрический заряд. В основу рассуждений положим соотношение

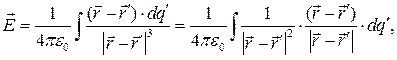(1)

где 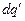- одно из выражени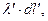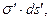й или 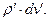Запишем выражения для радиус-векторов точки наблюдения и точки расположения физически бесконечно малого электрического заряда в форме

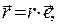
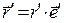, (2) где 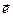и 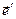- орты соответствующих направлений. Ниже будем считать, что выполнено условие 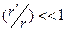, т.е. электрический заряд, создающий поле, сосредоточен в окрестности начала декартовой системы координат, а точки наблюдения выбираются достаточно далеко от начала координат. Разность радиус-векторов в числителе подынтегральной функции выражения (1) запишем в виде:

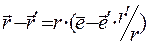(3)

Модуль этого выражения вычислим приближенно с учётом оговоренного выше условия с сохранением членов нулевого и первого порядка малости:

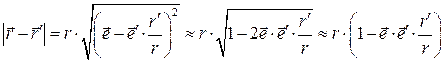. (4)

Выражение 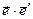равно косинусу угла между ортами рассматриваемых направлений. Знаменатель подынтегральной функции в соотношении (1) можно записать в форме:

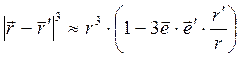. (5)

В итоге зависимость напряженности электростатического поля приобретает вид:

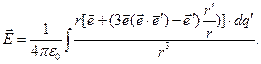(6)

В квадратных скобках числителя подынтегрального выражения (6) можно пренебречь слагаемым, пропорциональным отношению 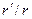, которое по условию является малой величиной. В результате приходим к соотношению

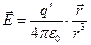. (7)

Физический результат при этом состоит в том, что электростатическое поле вдали от пространственно ограниченной системы распределенных зарядов аналогично полю, образованному совокупным электрическим зарядом, рассматриваемым как точечный заряд.