Принцип суперпозиции для вектора напряженности электростатического поля.

Принцип суперпозиции для вектора напряженности электростатического поля является прямым следствием принципа суперпозиции сил электрического взаимодействия неподвижных сосредоточенных зарядов, рассмотренного в разделе 2.1.

Напряжённость электростатического поля, созданного совокупностью неподвижных электрических зарядов в определенной точке пространства, равна векторной сумме напряженностей электрических полей, созданных отдельными зарядами в той же точке пространства независимо друг от друга.

Принцип суперпозиции справедлив в вакууме. В реальных средах и, в особенности в сильных электрических полях, он может нарушаться. Физические среды, в которых принцип суперпозиции для вектора напряженности электрического поля остаётся справедливым, называют линейными средами. Изучение электромагнитного поля в линейных средах будет продолжено в последующих разделах учебного пособия.

Математическая формулировка принципа суперпозиции имеет вид:

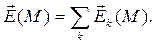(1)

Здесь М - рассматриваемая точка пространства, вектор 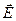- результирующая напряженность электрического поля, векторы суть напряженности слагаемых электрических полей, суммирование производится с учётом всех источников поля, включенных в систему, с использованием правила сложения векторных величин.

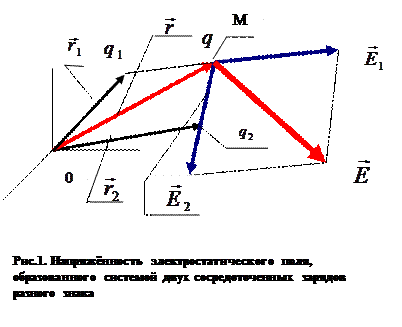
На приведенном рисунке 1 показано формирование результирующей напряженности электрического поля 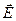в точке пространства М, образованного системой двух сосредоточенных зарядов, положительного заряда 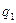и отрицательного заряда 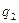, расположенных в точках пространства, описываемых радиус-векторам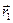и и соответственно. Пробный электрический заряд 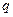по определению является положительным.

Принцип суперпозиции с успехом применяется и для определения напряжённости электростатического поля, создаваемого распределёнными зарядами. Если элементарный заряд , расположенный в некоторой точке пространства 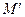, создаёт в рассматриваемой точке М пространства элементарную напряженность электростатического поля 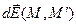, то результирующая напряжённость электростатического поля в точке М равна:

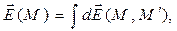(2)

интегрирование в этой формуле распространяется на всю совокупность зарядов, создающих электростатическое поле, а положение точки наблюдения М играет роль параметра. Физики при этом говорят, что интегрирование в конечном итоге проводится по координатам точек 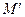расположения зарядов, образующих электростатическое поле.

Рассмотрим несколько примеров применения принципа суперпозиции для вектора напряжённости электростатического поля. Напряженность электростатического поля 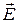, образованного единичным точечным зарядом 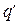, известна. Если в системе имеется 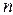электрических точечных зарядов 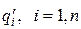, то напряженность результирующего поля 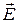в точке наблюдения определяется как векторная сумма напряжённостей полей , образованных каждым из зарядов в отдельности:

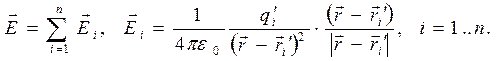(3)

Здесь 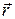- радиус-вектор точки наблюдения, 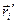- радиус-вектор точки расположения электрического заряда 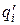. В проекциях на оси декартовой системы координат имеют место соотношения:

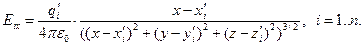
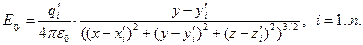(4)

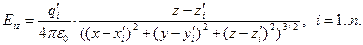
Для направляющих косинусов вектора 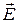имеем:

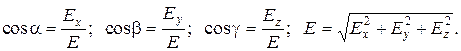( 5)

Еще раз подчеркнем, что при сложении электростатических полей отдельно алгебраически “складываются” проекции вектора 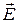и только потом вычисляется модуль полученного вектора.

При непрерывном распределении электрического заряда заряд в элементарном физически бесконечно малом объёме, на элементе площади поверхности или на элементе длины пространственной кривой можно считать сосредоточенным зарядом. Этот заряд создает в пространстве элементарное электростатическое поле

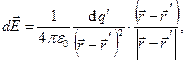( 6)

здесь 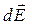- дифференциал (элемент, бесконечно малая часть) вектора напряженности электростатического поля в точке наблюдения с радиус-вектором 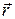, создаваемого элементарным зарядом , расположенным в точке пространства, описываемой радиус-вектором 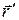. Остается только просуммировать выражение (6) по всем элементарным зарядам системы. Формальное решение задачи имеет вид:

для заряженного объема,

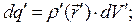
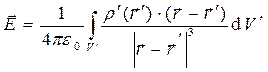(7)

для заряженной поверхности,

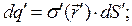
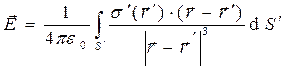(8)

для заряженной линии конечных или бесконечных размеров

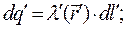
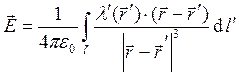. (9)

Физический смысл соотношений (3), (7), (8) и (9) состоит в том, что при известном расположении зарядов в пространстве (дискретное или непрерывное распределение) напряженность электростатического поля 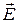может быть вычислена для произвольной точки пространства. Современное математическое обеспечение персональных компьютеров значительно облегчает конкретные расчеты поля неподвижных зарядов по заданному пространственному распределению последних.