Комплексное сопротивление параллельного контура первого вида

Поскольку 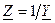, то с учётом (12.1) найдём нормированное комплексное сопротивление параллельного контура (рис. 12.4) в режиме холостого хода, используя в качестве нормирующего значения резонансное сопротивление контура ,

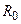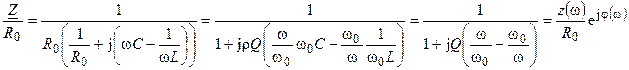
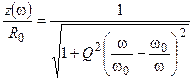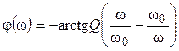где и — модуль и аргумент нормированного сопротивления параллельного контура.

Сравнивая нормированные комплексные сопротивления параллельного и последовательного контуров, видно, что их модули — обратно пропорциональны друг другу, а аргументы — противоположны по знаку.

На рис. 12.5 показаны частотные зависимости модуля (рис. 12.5, а) и аргумент нормированного комплексного сопротивления параллельного контура (рис. 12.5, б). Из частотной зависимости аргумента следует, что на резонансной частоте 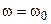сопротивление параллельного колебательного контура имеет резистивный (активный) характер, на частоте меньше резонансной — резистивно-индуктивный характер ( 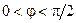), а на частоте больше резонансной — резистивно-емкостной характер ( ).

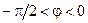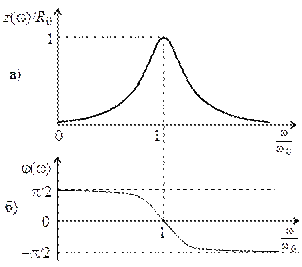
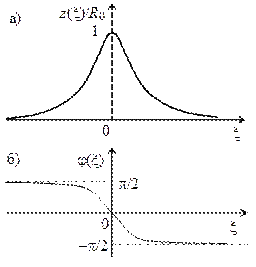
Рис. 12.5 Рис. 12.6

Используя понятие обобщённой расстройки 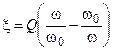, получаем

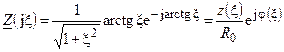
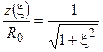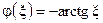где и — модуль и аргумент сопротивления контура, выраженные через обобщённую расстройку, вид которых (рис. 12.6) совпадает с аналогичными зависимостями нормированного тока последовательного контура (см. рис. 11.7).

Определим нормированную комплексную амплитуду напряжения на контуре, используя найденное ранее значение этой амплитуды на резонансной частоте 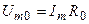как нормирующее значение,

.

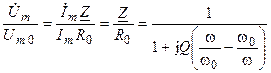Найденная комплексная характеристика параллельного контура совпадает с его нормированным комплексным сопротивлением.