Комплексный коэффициент передачи последовательного контура
Определим комплексный коэффициент передачи последовательного контура (рис. 11.2, а) по напряжению в режиме холостого хода в случае, когда выходное напряжение снимается с индуктивности,
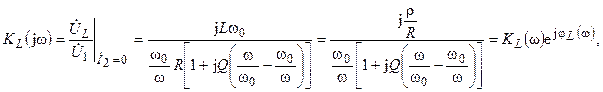
где 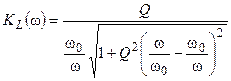 и
и 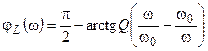 — модуль и аргумент комплексного коэффициента передачи, которые определяют АЧХ и ФЧХ контура соответственно
— модуль и аргумент комплексного коэффициента передачи, которые определяют АЧХ и ФЧХ контура соответственно
Аналогичным образом определим комплексный коэффициент передачи контура в режиме холостого хода в случае, когда выходное напряжение снимается с ёмкости (рис. 11.2, б),
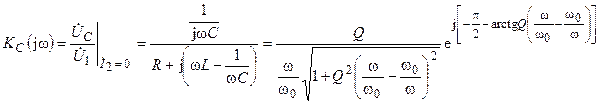 .
.
В данном случае АЧХ и ФЧХ контура будут иметь вид
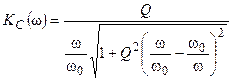 ;
; 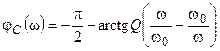 .
.
Проанализируем найденные частотные характеристики последовательного колебательного контура. При подаче на контур постоянного напряжения имеющего частоту  , напряжение на индуктивности будет равно нулю
, напряжение на индуктивности будет равно нулю 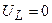 , поскольку её сопротивление равно нулю, и модуль коэффициента передачи
, поскольку её сопротивление равно нулю, и модуль коэффициента передачи 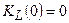 . При этом напряжения на ёмкости будет равно входному напряжению, поскольку на постоянно токе сопротивление ёмкости бесконечно велико, и модуль коэффициента передачи
. При этом напряжения на ёмкости будет равно входному напряжению, поскольку на постоянно токе сопротивление ёмкости бесконечно велико, и модуль коэффициента передачи 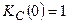 .
.
На резонансной частоте 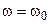 модули обоих коэффициентов передачи равны добротности контура
модули обоих коэффициентов передачи равны добротности контура 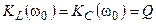 . В результате, при резонансе амплитуда напряжения на реактивных элементах контура в
. В результате, при резонансе амплитуда напряжения на реактивных элементах контура в 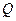 раз превышает амплитуду входного напряжения.
раз превышает амплитуду входного напряжения.
На бесконечно большой частоте 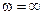 сопротивление индуктивности бесконечно велико, поэтому напряжение на ней будет равно входному напряжению и
сопротивление индуктивности бесконечно велико, поэтому напряжение на ней будет равно входному напряжению и 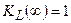 . На той же частоте сопротивление ёмкости будет равно нулю и поэтому
. На той же частоте сопротивление ёмкости будет равно нулю и поэтому 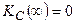 .
.
Проанализируем положение максимумов найденных АЧХ колебательного контура.
Преобразуем АЧХ контура в случае, когда выходное напряжение снимается с индуктивности,
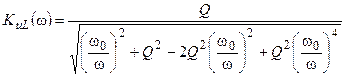 .
.
Определим частоту, соответствующую максимуму рассматриваемой функции, решая уравнение
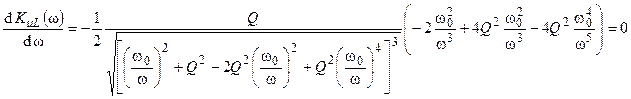 ,
,
которое сводится к виду:
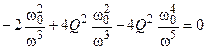 ;
;
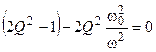 .
.
Решая последнее уравнение, находим искомую частоту, учитывая, что физический смысл имеет только её положительное значение,
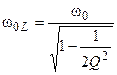 .
.
Подставляя найденное значение частоты в функцию 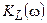 , находим её максимум АЧХ
, находим её максимум АЧХ
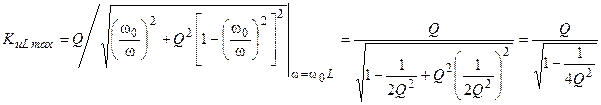 .
.
Выполняя аналогичный анализ АЧХ контура в случае, когда выходное напряжение снимается с ёмкости, находим частоту соответствующую её максимуму
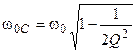 ,
, 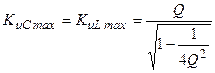 .
.
Из найденных выражений следует, что максимум функции 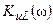 располагается на частоте больше резонансной
располагается на частоте больше резонансной 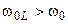 , а максимум функции
, а максимум функции 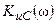 — на частоте меньше резонансной
— на частоте меньше резонансной 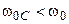 . При этом максимумы обеих АЧХ превышают значение добротности
. При этом максимумы обеих АЧХ превышают значение добротности 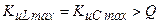 . Однако, поскольку в радиотехнических устройствах обычно используются колебательный контура с добротностью не менее
. Однако, поскольку в радиотехнических устройствах обычно используются колебательный контура с добротностью не менее 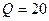 , то отклонения частот
, то отклонения частот 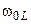 и
и 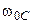 от резонансной частоты
от резонансной частоты 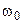 и максимумов АЧХ от значения добротности пренебрежимо малы, поэтому обычно полагают, что
и максимумов АЧХ от значения добротности пренебрежимо малы, поэтому обычно полагают, что 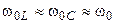 и
и 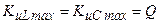 .
.
Частотные характеристики последовательного колебательного контура, построенные с учётом результатов выполненного анализа, показаны на рис. 11.8. На резонансной частоте 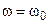 АЧХ пересекаются в точке с координатами
АЧХ пересекаются в точке с координатами 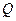 и
и 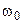 .
.
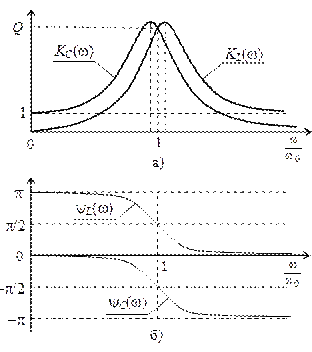
Рис. 11.8
Частотная избирательность последовательного колебательного контура проявляется в том, что, если на контура подать воздействие в виде суммы гармонических колебаний, имеющих одинаковые амплитуды и различные частоты, то его на выходе амплитуды колебаний, частота которых близка к резонансной частоте контура значительно превышают амплитуды колебаний, частоты которых отличаются от резонансной. При этом говорят, что колебательный контур пропускает» колебания одних частот и не пропускает колебания других частот.
11.6. Влияние сопротивления источника энергии и нагрузки на характеристики
последовательного контура
Пусть контур питается от источника напряжения с конечным внутренним сопротивлением 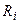 и нагружен сопротивлением нагрузки
и нагружен сопротивлением нагрузки 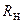 , подключённым параллельно индуктивности контура, (рис. 11.9, а).
, подключённым параллельно индуктивности контура, (рис. 11.9, а).
Пересчитаем параллельное соединение сопротивления нагрузки и индуктивности в эквивалентное последовательное соединение при резонансе
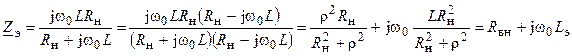 .
.
где 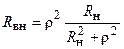 — вносимое сопротивление;
— вносимое сопротивление; 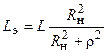 — эквивалентная индуктивность контура.
— эквивалентная индуктивность контура.

а) б) в)
Рис. 11.9
Если сопротивление нагрузки выбрать из условия 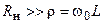 , то
, то 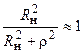 и тогда:
и тогда:
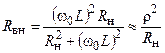 ;
; 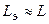 .
.
Из полученных выражений следует, что, если сопротивление нагрузки достаточно велико по сравнению с характеристическим сопротивлением контура, то влияние нагрузки на контур выражается только в том, что увеличиваются потери контура. При этом индуктивность контура, и, следовательно, его резонансная частота практически не изменяются.
Определим эквивалентная добротность контура с учётом вносимого сопротивления
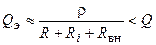 .
.
Видно, что влияние внутреннего сопротивления источника напряжения и вносимого сопротивления выражается в уменьшении эквивалентной добротность контура, что вызывает расширение полосы пропускания и ухудшение частотной избирательности контура.
Поэтому для поддержания высокой частотной избирательности последовательного колебательного контура необходимо уменьшать внутреннее сопротивление 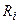 источника входного напряжения и увеличивать сопротивление нагрузки
источника входного напряжения и увеличивать сопротивление нагрузки 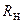 .
.
Можно показать, что аналогичный результат имеет место, если сопротивление нагрузки подключить параллельно емкости последовательного контура (рис. 11.9, б)
Для уменьшения влияния сопротивления нагрузки 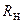 на частотные характеристики последовательного колебательного контура используется частичное включение нагрузки, при котором её подключают к части реактивного сопротивления контура. Наиболее просто частичное включение нагрузки реализуется с помощью катушки индуктивности, имеющей отвод от части витков, (рис. 11.9, в). Если катушка индуктивности имеет
на частотные характеристики последовательного колебательного контура используется частичное включение нагрузки, при котором её подключают к части реактивного сопротивления контура. Наиболее просто частичное включение нагрузки реализуется с помощью катушки индуктивности, имеющей отвод от части витков, (рис. 11.9, в). Если катушка индуктивности имеет 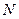 витков, к части которых
витков, к части которых 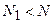 подключено сопротивление нагрузки, то при резонансе сопротивление этой части катушки будет
подключено сопротивление нагрузки, то при резонансе сопротивление этой части катушки будет 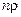 , где
, где 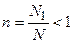 — коэффициент включения нагрузки. В результате, вносимое сопротивление уменьшается до величины
— коэффициент включения нагрузки. В результате, вносимое сопротивление уменьшается до величины
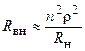 .
.
Лекция № 14
Дата добавления: 2017-09-01; просмотров: 5507;











