Виды расстроек и полоса пропускания последовательного контура
При анализе частотных характеристик колебательных контуров используется понятие обобщенной расстройки
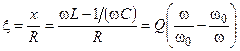 .
.
Нулевое значение обобщённой настройка 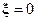 соответствует резонансной частоте контура
соответствует резонансной частоте контура 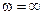 , отрицательные значения
, отрицательные значения 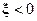 — частотам ниже резонансной
— частотам ниже резонансной 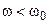 , а положительные значения
, а положительные значения 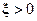 — частотам выше резонансной
— частотам выше резонансной 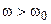 . Нулевой частоте
. Нулевой частоте  соответствует значение обобщённой настройка
соответствует значение обобщённой настройка 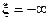 , а бесконечно большой частот
, а бесконечно большой частот 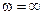 — значение
— значение  .
.
Используя обобщённую настройку, можно нормированные частотные характеристики тока контура представить в виде:
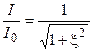 ;
;
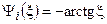 .
.
Зависимость модуля и аргумента нормированного тока последовательного контура от обобщенной расстройки показаны на рис. 11.7.
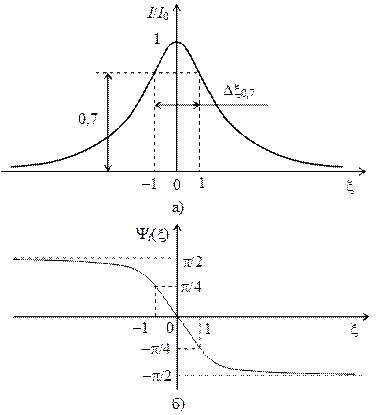
Рис. 11.7
Использование обобщённой настройки позволяет перенести область частот, соответствующую резонансу, в начало координат, а также представить семейство характеристик, соответствующих контурам с различными добротностями и резонансными частотами настройки, в виде одно функции переменной 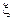
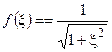 .
.
При анализе частотных характеристик колебательных контуров в области частот вблизи резонансной частоты обычно используется следующее приближенное равенство
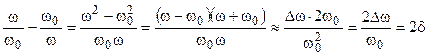 ,
,
где 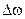 =
= 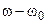 — абсолютной расстройкой контура, которая положительна при
— абсолютной расстройкой контура, которая положительна при 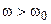 и отрицательна при
и отрицательна при 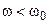 ;
; 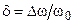 — относительной расстройкой контура.
— относительной расстройкой контура.
Тогда вблизи резонансной частоты 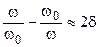 , а обобщенная расстройка
, а обобщенная расстройка 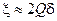 .
.
С учётом последнего соотношения нормированные входные частотные характеристик контура можно записать в виде:
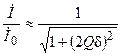 ;
;
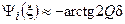 .
.
Полученные выражения достаточно точно описывают частотные характеристики при малых расстройках 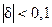 .
.
Полоса частот близи резонанса, на границах которой ток контура уменьшается до уровня 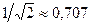 относительно максимального значения называется полосой пропускания контура и обозначается в виде
относительно максимального значения называется полосой пропускания контура и обозначается в виде  .
.
Тогда на границах полосы должно выполняться следующее условие
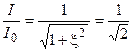 .
.
Решая полученное уравнение, находим границы полосы пропускания: 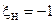 — нижняя граница и
— нижняя граница и 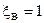 — верхняя граница. Тогда полоса пропускания контура на уровне
— верхняя граница. Тогда полоса пропускания контура на уровне 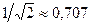 , выраженная через обобщённую расстройку, будет равна
, выраженная через обобщённую расстройку, будет равна  . На рис. 11.7 границы полосы пропускания указаны пунктирными линиями. При этом ФЧХ на границах полосы пропускания имеет следующие значения
. На рис. 11.7 границы полосы пропускания указаны пунктирными линиями. При этом ФЧХ на границах полосы пропускания имеет следующие значения
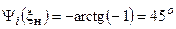 ;
; 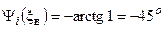 .
.
Подставляя граничные значения 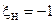 и
и 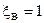 в общее выражение обобщённой расстройки
в общее выражение обобщённой расстройки 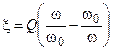 , получаем уравнения для определения граничных частот
, получаем уравнения для определения граничных частот 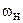 ,
, 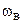 полосы пропускания на уровне
полосы пропускания на уровне 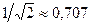 :
:
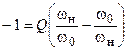 ,
,
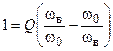 ,
,
которые преобразуются к виду
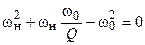 ,
,
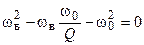 .
.
Решая уравнения, находим граничных частот полосы пропускания:
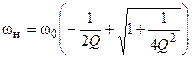 ,
,
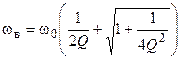 .
.
Определяем полосу пропускания контура на уровне на уровне 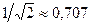 , выраженную в герцах:
, выраженную в герцах:
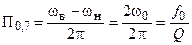 .
.
Полученное соотношение часто используется для оценки добротности контура путём экспериментального измерения резонансной частоты 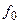 и полосы пропускания
и полосы пропускания  контура, зная которые, определяют добротности контура по формуле
контура, зная которые, определяют добротности контура по формуле
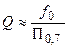 .
.
Дата добавления: 2017-09-01; просмотров: 5505;











