Резонансная частота и волновое сопротивление последовательного контура
 Рассмотрим работу последовательного колебательного контура (рис. 11.1) при воздействии на него идеального источника гармонической э.д.с.
Рассмотрим работу последовательного колебательного контура (рис. 11.1) при воздействии на него идеального источника гармонической э.д.с. 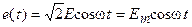 .
.
Определим комплексное сопротивление контура
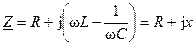 ,
,
где 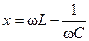 — мнимая составляющая сопротивления
— мнимая составляющая сопротивления
Поскольку при резонансе напряжений мнимая составляющая сопротивления контура равна нулю 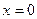 , то на резонансной частоте
, то на резонансной частоте 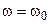 получаем следующее уравнение
получаем следующее уравнение
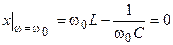 ,
,
решая которое находим угловую резонансную частоту
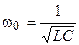 .
.
Угловой частоте 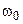 соответствует обычная частота
соответствует обычная частота
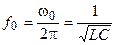 .
.
Из полученного выражения следует, что резонансная частота колебательного контура зависит только от параметров реактивных элементов контура 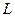 ,
, 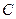 и её можно изменять с помощью перестраиваемых индуктивностей и ёмкостей.
и её можно изменять с помощью перестраиваемых индуктивностей и ёмкостей.
Если частота э.д.с. источника напряжения, действующего в контуре, совпадает с резонансной частотой контура, то такой контур называют настроенным. В противном случае контур называется расстроенным.
Используя выражение для резонансной частоты контура, можно индуктивность контура выразить через ёмкость и наоборот:
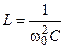 ,
, 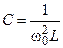 .
.
Из условия резонанса 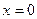 следует, что на резонансной частоте реактивное сопротивление емкости равно реактивному сопротивлению индуктивности. Данное значение сопротивления называется волновым (характеристическим) сопротивление контура, которое можно определить в следующем виде
следует, что на резонансной частоте реактивное сопротивление емкости равно реактивному сопротивлению индуктивности. Данное значение сопротивления называется волновым (характеристическим) сопротивление контура, которое можно определить в следующем виде
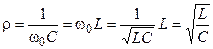 .
.
Таким образом, на резонансной частоте сопротивление последовательного контура является активным 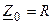 . При этом комплексная и вещественная амплитуды тока контура будут иметь вид
. При этом комплексная и вещественная амплитуды тока контура будут иметь вид
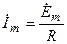 ,
, 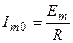
и ток в вещественной форме
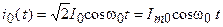 .
.
где 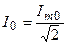 — действующее значение тока контура при резонансе.
— действующее значение тока контура при резонансе.
При расстройке контура модуль его сопротивления 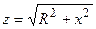 увеличивается, что вызывает уменьшение амплитуды тока
увеличивается, что вызывает уменьшение амплитуды тока
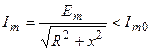 .
.
Поскольку на резонансной частоте сопротивления реактивных элементов контура равны и через них проходит один и тот же ток, то амплитуды напряжения на этих элементах будут также равны:
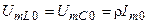 .
.
Дата добавления: 2017-09-01; просмотров: 4531;











