Понятие взаимной индукции и взаимной индуктивности
Если две катушки индуктивности, которые расположены соосно, то есть совпадают их оси, и так, что часть магнитного потока, вызванного током одной из катушек, пронизывает витки другой катушки (рис. 9.1), то они называются индуктивно связанными.
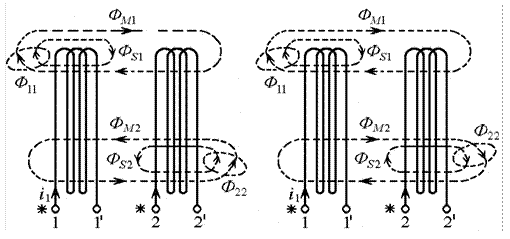
а) б)
Рис. 9.1
Пусть токи 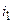 и
и 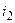 первой и второй катушек вызывают магнитные потоки самоиндукции
первой и второй катушек вызывают магнитные потоки самоиндукции 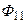 и
и 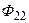 соответственно. Тогда часть магнитного потока самоиндукции
соответственно. Тогда часть магнитного потока самоиндукции 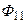 первой катушки, которая пронизывает витки второй катушки, называется магнитным потоком взаимоиндукции
первой катушки, которая пронизывает витки второй катушки, называется магнитным потоком взаимоиндукции 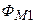 (
( 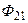 ) второй катушки. Оставшаяся часть магнитного потока
) второй катушки. Оставшаяся часть магнитного потока 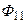 самоиндукции первой катушки называется магнитным потоком рассеяния
самоиндукции первой катушки называется магнитным потоком рассеяния 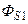 первой катушки. Аналогичным образом для второй катушки:
первой катушки. Аналогичным образом для второй катушки: 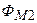 (
( 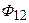 ) — магнитный поток взаимоиндукции первой катушки и
) — магнитный поток взаимоиндукции первой катушки и 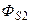 — магнитный поток рассеяния второй катушки.
— магнитный поток рассеяния второй катушки.
Тогда магнитный поток самоиндукции каждой из катушек можно представить в виде суммы двух составляющих:
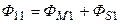 ,
,
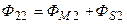 .
.
а полные магнитные потоки — в виде суммы магнитных потоков самоиндукции и взаимоиндукции:
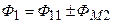 ;
;
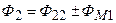 .
.
Аналогичным образом можно представить полные потокосцепления катушек:
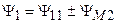 ;
;
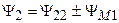 .
.
где 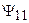 и
и 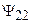 — потокосцепления самоиндукции первой и второй катушек, обусловленные их собственными токами;
— потокосцепления самоиндукции первой и второй катушек, обусловленные их собственными токами; 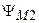 — потокосцепление взаимоиндукции первой катушки, обусловленное током второй катушки;
— потокосцепление взаимоиндукции первой катушки, обусловленное током второй катушки; 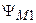 — потокосцепление взаимоиндукции второй катушки, обусловленное током первой катушки.
— потокосцепление взаимоиндукции второй катушки, обусловленное током первой катушки.
Знак «плюс» в последних уравнениях соответствует одинаковому направлению магнитных потоков самоиндукции и взаимоиндукции в каждой из катушек. В этом случае включение катушек называется согласным(рис. 9.1, а).
Знак «минус» соответствует встречному направлению потоков самоиндукции и взаимоиндукции в катушке. В этом случае включение катушек называется встречным(рис. 9.1, б).
В соответствии с законом электромагнитной индукции Фарадея, э.д.с., наводимые в каждой из индуктивно связанных катушек:
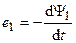 ,
,
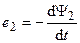 .
.
Тогда напряжения на выводах катушек:
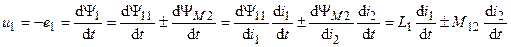 ;
;
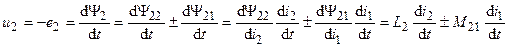 ,
,
где 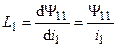 и
и 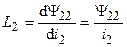 — собственные индуктивности катушек;
— собственные индуктивности катушек; 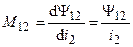 и
и 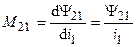 — взаимные индуктивности катушек.
— взаимные индуктивности катушек.
Для линейных катушек индуктивности всегда выполняется условие
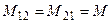 .
.
В Международной системе единиц СИ взаимная индуктивность 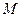 , как и собственная индуктивность
, как и собственная индуктивность 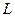 катушек измеряется в генри (Гн).
катушек измеряется в генри (Гн).
С учетом введенных обозначений получаем следующие зависимости напряжений на выводах индуктивно связанных катушек от протекающих в них токов:
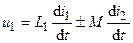 ;
;
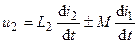 ,
,
где 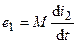 и
и 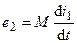 — э.д.с. взаимоиндукции.
— э.д.с. взаимоиндукции.
Отсюда следует, что напряжения на каждой из индуктивно связанных катушек, помимо падения напряжения, вызванного собственным током катушке, содержит дополнительную составляющую, вызываемую током, протекающим в другой катушке. При согласном включении катушек напряжения катушек увеличиваются на значение э.д.с. взаимоиндукции и эти э.д.с. записываются в уравнения со знаком плюс, а при встречном включении уменьшается на значение этих же э.д.с., которые в этом случае записываются в уравнения со знаком минус.
При гармоническом воздействии уравнения индуктивно связанных катушек могут быть записаны в комплексной форме:

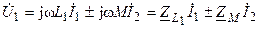 ;
;
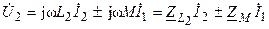 .
.
где 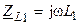 и
и 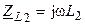 — собственные комплексные сопротивления катушек;
— собственные комплексные сопротивления катушек; 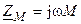 — взаимное комплексное сопротивление катушек.
— взаимное комплексное сопротивление катушек.
На основании полученных уравнений в комплексной форме можно составить эквивалентную схему замещения индуктивно связанных катушек (рис. 9.2), которая не содержит взаимных индуктивностей, а их влияние учтено включением в схему замещения источников напряжения, имеющих э.д.с. 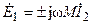 и
и 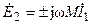 , обусловленные взаимной индукцией.
, обусловленные взаимной индукцией.
Если катушки расположены не соосно, то есть угол между их осями 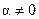 , то взаимная индуктивность уменьшается до значения
, то взаимная индуктивность уменьшается до значения 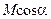 и при
и при 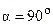 будет равна нулю. В этом случае магнитные потоки самоиндукции и взаимной индукции в катушках будут перпендикулярны друг другу, то есть ортогональны. Однако в реальных катушках получить идеальную ортогональность указанных магнитных потоком во всем пространстве вокруг витков индуктивно связанных катушек практически невозможно.
будет равна нулю. В этом случае магнитные потоки самоиндукции и взаимной индукции в катушках будут перпендикулярны друг другу, то есть ортогональны. Однако в реальных катушках получить идеальную ортогональность указанных магнитных потоком во всем пространстве вокруг витков индуктивно связанных катушек практически невозможно.
Для различия согласного и встречного включения включение индуктивно связанных катушек вводят понятие одноимённых зажимов связанных катушек индуктивности.
Одноимёнными выводами двух индуктивно связанных катушек называются выводы, выбранные так, что при одинаковом направлении токов относительно этих выводов магнитные потоки самоиндукции и взаимной индукции совпадают, что обеспечивает согласное включение катушек. На электрических схемах одноимёнными выводы обозначают знаками в виде звёздочки «*», треугольника «D», жирной точки «·» и т. п. (рис. 9.3).
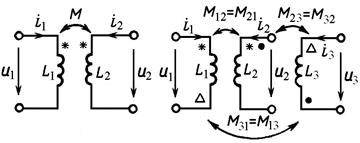
а) б)
Рис. 9.3
Дата добавления: 2017-09-01; просмотров: 3599;











