Понятие о комплексных характеристиках цепи

Комплексной характеристикой электрической цепи называется отношение комплексного изображения её реакции к комплексному изображению внешнего воздействия.

Ранее было показано, что в случае гармонического внешнего воздействияв качестве комплексных изображений воздействия и реакции цепи используют либо комплексные амплитуды, либо комплексные действующие значения напряжений и токов цепи.

Комплексные характеристики цепи делятся на входные и передаточные.

Комплексной входной характеристикой цепи называется отношение комплексных изображений реакции цепи и внешнее воздействие на одноимённых выводах цепи.

Комплексной передаточной характеристикойцепи называются отношение комплексных изображений реакции цепи и внешнее воздействие на разноимённых выводах цепи.

Размерность комплексной передаточной характеристики определяется отношению размерностей реакции и внешнего воздействия. Поскольку в электрической цепи реакциями и воздействиями являются токи и напряжения, то комплексная характеристика может иметь размерность сопротивления и проводимости, когда реакция и воздействие имеют разные размерности, или быть безразмерной величиной, когда реакция и воздействие имеют одинаковую размерность.

Рассмотрим комплексные характеристики электрической цепи на примере линейного пассивного четырехполюсника (рис. 10.1).

Выводы (полюса) 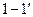чётырёхполюсника, к которым подключён источник энергии, задающий внешнее воздействие, будем называть входными, а выводы 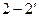, к которым подключена нагрузка нагрузки, — выходными.

К комплексным входным характеристикам четырёхполюсника относятся комплексные сопротивления 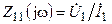и 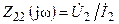и комплексные проводимости, 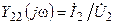, определяемых относительно выводов 1, 1’ и 1, 2’ соответственно

К комплексным передаточным характеристикам четырёхполюсника относятся:

¾ 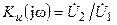— комплексный коэффициент передачи по напряжению;

¾ 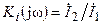— комплексный коэффициент передачи по току;

¾ 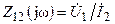, 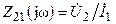— комплексные передаточные сопротивления;

¾ 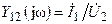, 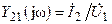— комплексные передаточные проводимости.

В общем виде комплексная характеристика может быть записана в показательной .форме

,

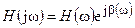где 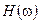— модуль комплексной характеристики, который равен отношению амплитуд или действующих значений реакции и внешнего воздействия; 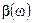— аргумент комплексной характеристики, который представляет собой разность начальных фаз реакции и внешнего воздействия.

Зависимость модуля комплексной передаточной характеристики от частоты называетсяамплитудно-частотной характеристикой (АЧХ) цепи, а зависимость её аргумента от частота — фазочастотной характеристикой (ФЧХ) цепи. Таким образом, комплексные передаточные характеристики цепи сочетает в себе АЧХ и ФЧХ цепи.

Зависимости модуля и аргумента входных комплексных характеристик от частоты называются обычно просто частотными зависимостями.

10.2. Комплексные характеристики простейших RL- и RC-четырёхполюсников с одним реактивным элементом

На рис. рис. 10.2, а, б изображены схемы простейших RL- и RC-четырёхполюсников с одним реактивным элементом, а на рис. 10.2, в — обобщенная схема четырёхполюсников.

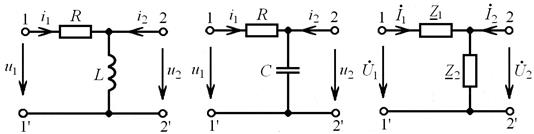
а) б) в)

Рис. 10.2

Определим комплексное входное сопротивление обобщенной схемы (рис. 10.2 в) в режиме холостого хода

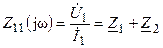
и комплексный коэффициент передачи по напряжению

,

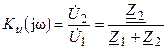где .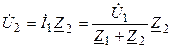

В режиме короткого замыкания входное сопротивление цепи 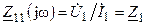, а коэффициент передачи по напряжению .

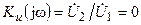В качестве примера определим комплексные характеристики RL-четырёхполюсника (рис. 10.2, а) в режиме холостого хода.

Найдём входное комплексное сопротивление RL-четырёхполюсника в режиме холостого хода

,

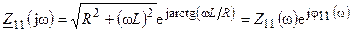где 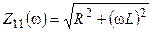и 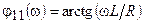— модуль и аргумент комплексного сопротивления.

Частотные зависимости модуля и аргумента комплексного входного сопротивления показаны на рис. 10.3. На низких частотах, когда сопротивление индуктивности существенно меньше 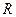, входное сопротивление цепи имеет характер, близкий к активному (резистивному). При этом фазовый сдвиг между напряжением 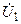и током 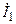близок к 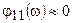. На высоких частотах, частоты, когда сопротивление индуктивности существенно больше 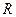, входное сопротивление цепи имеет характер, близкий к индуктивному, а фазовый сдвиг между напряжением 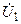и ток 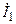приближается к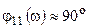

Найдем комплексный коэффициент передачи по напряжению RL-четырёхполюсника

.

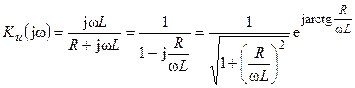где 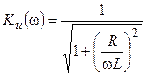— АЧХ и 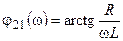— ФЧХ:

Найденные АЧХ и ФЧХ изображены на рис. 10.4. Напряжения на элементах RL-четырёхполюсника (рис. 10.2, а) пропорциональны их сопротивлениям. Так как на низких частотах сопротивление индуктивности 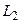мало по сравнению с R, то напряжение на индуктивности также мало по сравнению с напряжением на сопротивлении R. В результате, на этих частотах АЧХ четырёхполюсника близка к нулю. При этом фазовый сдвиг между напряжением 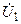и током близок к нулю. Однако напряжение 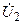на индуктивности, которое является выходным напряжение четырёхполюсника, опережает по фазе ток 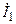на 90^о. В результате, ФЧХ четырёхполюсника на низких частотах близка к 90^о.

С ростом частоты сопротивление индуктивности увеличивается и вследствие этого распределение напряжений между элементами четырёхполюсника также изменяется. На достаточно высоких частотах сопротивление индуктивности 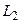много больше R. При этом практически все входное напряжение оказывается приложенным к индуктивности, и выходное напряжение практически 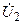почти совпадает с входным напряжением 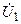. В результате, на высоких частотах АЧХ становится близкой к единице, а ФЧХ — к нулю.

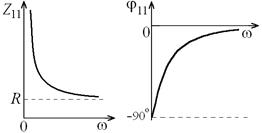
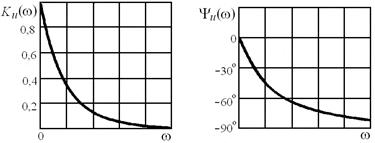
Аналогичный анализ RC-четырёхполюсника (рис. 10.2) показывает, что частотные зависимости модуля и аргумента его комплексного входного сопротивления (рис. 10.5), а также АЧХ и ФЧХ (рис.10.6) дуальны аналогичным зависимостям RL-четырёхполюсника.

а) б) а) б)

Рис. 10.5 Рис. 10.6

Таким образом, амплитудно-частотные характеристики пассивных линейных четырёхполюсников с одним реактивным элементом имеют вид монотонных функций. Поэтому амплитуда отклика таких цепей на гармоническое воздействие также изменяется монотонно при увеличении или уменьшении частоты воздействия.

Лекция № 12