Компонентные и топологические уравнения электрической цепи

Математическое описание процессов в сложных цепях, состоящих из большого числа элементов, основывается на компонентных и топологических уравнениях.

Компонентныминазываются уравнения, которые устанавливают зависимость между разнотипными переменными, относящиеся к одному из элементов цепи, например, уравнения (2.1), (2.5) и (2.10), связывающие ток и напряжение в пассивных элементах цепи , , .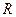

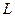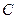Используя компонентные уравнения, можно составить уравнение, связывающие напряжение и ток любой ветви электрической цепи. Например, для ветви, показанной на рис. 3.5, такое уравнение будет иметь вид

.

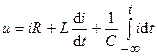Топологическиминазываются уравнения, которые устанавливают зависимость между однотипными переменными цепи, обусловленную структурой цепи, например, уравнения, которые устанавливают зависимость между токами либо между напряжениями ветвей цепи. Примером таких уравнений являются уравнения, которые составляются на основании законов Кирхгофа, сформулированные Густавом Кирхгофом в 1845 году.

Согласно первому закону Кирхгофаалгебраическая сумма токов ветвей, подключенных к одному и тому же узлу цепи, равна нулю

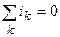, (3.1)

где 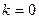— номер ветви, подключенной к рассматриваемому узлу; 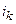— ток k-ой ветви.

При составлении уравнения (3.1) токи, направленные к узлу, записываются в уравнение со знаком «плюс», а токи, направленные от узла, — со знаком «минус». С физической точки зрения первый закон Кирхгофа выражает тот факт, что в узле электрической цепи невозможно ни накопления, ни исчезновение электрического заряда, то есть сколько электрических зарядов подходит к узлу, столько же и уходит от него за один и тот же промежуток времени.

Число независимых уравнений, которые можно составить по первому закону Кирхгофа, определяется числом независимых узлов цепи

,

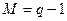где 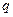— общее число узлов цепи.

Последний 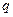-й узел является зависимым, поскольку уравнение, составленное для него по первому закону Кирхгофа, может быть получено путём линейного преобразования уравнений, составленных для остальных 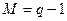узлов цепи.

Например, для узла цепи, показанной на рис. 3.6, уравнение, составленное по первому закону Кирхгофа, будет иметь вид

.

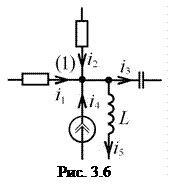
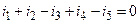Если в последнем уравнении токи, втекающие в узел, оставить в левой части уравнения, а токи, вытекающие из узла, перенести в правую части уравнения, то получим уравнение

,

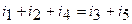в соответствии с которым первый закон Кирхгофа можно сформулировать следующим образом: в любой момент времени сумма токов, втекающих в узел, равна сумме токов, вытекающих из этого узел.

Второй закон Кирхгофагласит, что алгебраическая сумма напряжений на пассивных элементах и источниках тока, входящих в состав замкнутого контура электрической цепи, равна алгебраической сумме э.д.с. идеальных источников напряжения, действующих в этом контуре,

, (3.2)

где 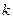— номер ветви; 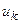— алгебраическая сумма напряжений на пассивных элементах и источнике тока, водящего в состав 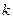-ой ветви; 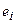— э.д.с. 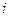-го идеального источника напряжения, действующего в контуре.

Если направление напряжения на элементе ветви контура совпадает с направлением обхода контура, то оно записываются в левую часть уравнения (3.2) со знаком «плюс», в противном случае оно записывается со знаком «минус». Аналогичным образом записываются в правую часть уравнения (3.2) э.д.с. идеальных источников напряжения, действующих в контуре.

С физической точки зрения второй закон Кирхгофа выражает тот факт, что работа по перемещению единичного электрического заряда по замкнутому контуру цепи равна нулю.

Число независимых уравнений, которые можно составить по второму закону Кирхгофа равно число независимых контуров цепи, которое, в свою очередь, определяется числом главных ветвей графа цепи,

,

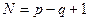где 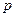и 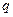— общее число ветвей и узлов электрической цепи соответственно.

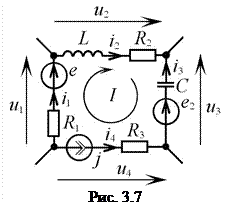
Например, для контура электрической цепи (рис. 3.7) уравнение, составленное по второму закону Кирхгофа, будет иметь вид

,

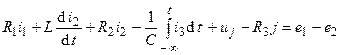где 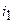, , 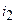, 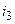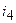— токи ветвей; 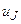— напряжение на источнике тока 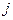, действующем в 4-ой ветв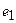и; и 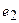— э.д.с. источников напряжения, действующих в контуре.

Перегруппировав слагаемые в (3.2), можно записать второй закон Кирхгофа в виде

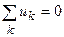, (3.3)

где 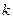— номер ветви контура; 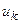— напряжение 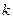-ой ветви, которое. определяется как алгебраическая сумма напряжений на пассивных элементах, а также на источниках тока и э.д.с., входящих в состав 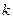-ой ветви

В соответствии с уравнением (3.3) второй закон Кирхгофа можно сформулировать следующим образом. Алгебраическая сумма напряжений ветвей, образующих замкнутый контур электрической цепи, равна нулю.

Напряжения ветвей, направления которых совпадают с направлением обхода контура, подставляют в уравнение (3.3) со знаком «плюс», а не совпадающие — со знаком «минус». Уравнения (3.2) и (3.3) идентичны. Для расчётов уравнение (3.2) является более удобным, поскольку в нём неизвестные напряжения на пассивных элементах и источниках тока записаны в левой части уравнения, а известные э.д.с. источников напряжения — в правой части уравнения, что уменьшает вероятность ошибок при составлении уравнений.