Уравнение постоянства расхода жидкости

При условии непроницаемости и недеформируемости стенок трубопровода и отсутствия разрывов и пустот для стационарного потока жидкости ее массовый расход постоянен.

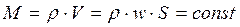– уравнение постоянства расхода жидкости.

В любых поперечных сечениях стационарного потока жидкостей ее массовый расход постоянен.

Это уравнение выражается материальным балансом потока и является частным случаем закона сохранения массы.

Для несжимаемой жидкости: ρ₁=ρ₂=ρ=const

В этом случае:

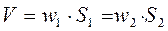. Отсюда следует,

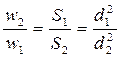– важное для практики следствие из уравнения постоянства расхода.

Средняя скорость обратно пропорциональна живому сечению потока или квадрату диаметра трубы.

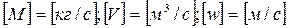
Уравнение Бернулли

В 1738 году швейцарский ученый Д. Бернулли получил уравнение:

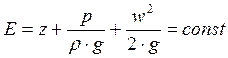– уравнение Бернулли для стационарного потока идеальной (невязкой) жидкости

w – средняя скорость потока;

р – гидростатическое давление;

z – геометрический напор, т.е. удельная потенциальная энергия геометрического положения потока жидкости в данном сечении(м);

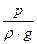– статический или пьезометрический напор, т.е. удельная потенциальная энергия гидростатического давления жидкости на данном уровне (м) ;

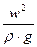– скоростной или динамический напор, т.е. удельная кинетическая энергия потока жидкости в данном сечении (м);

Е – полный гидродинамический напор, полная удельная механическая энергия потока жидкости в данном сечении.

В любых поперечных сечениях стационарного потока идеальной (невязкой) жидкости полный гидродинамический напор постоянен, т.е. полная удельная механическая энергия потока жидкости постоянна по длине труба.

Уравнение Бернулли выражает энергетический баланс потока и является частным случаем закона сохранения энергии.

Напор – удельная весовая механическая энергия потока жидкости.

Уравнение Бернулли можно записать иначе, если умножить обе его части на величину ρ·g:

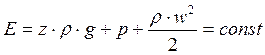
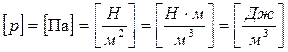
р – механическая энергия единицы объема жидкости (потока).

Уравнение Бернулли можно применять для реальной (вязкой) жидкости:

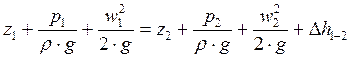
Δh_1-2 – потеря напора потока на участке трубы между сечениями 1-1 и 2-2.

Потерянный напор расходуется на преодоление гидравлического сопротивления трубопровода. Последнее складывается из потерь на трение между слоями жидкости, между жидкостью и стенками трубы, а так же в местных сопротивлениях (резкий поворот трубы, внезапное изменение сечения потока, запорно-регулирующая арматура и т.д.).

При этом часть удельной потенциальной энергии жидкости превращается в тепловую энергию и рассеивается в окружающем пространстве.

Рассмотрим диаграмму Бернулли:

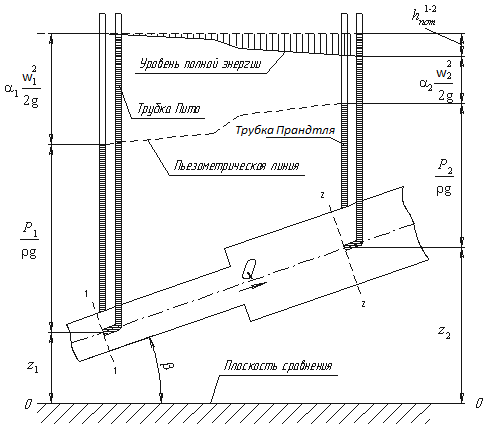
Трубки Пито и Прандтля называют пьезометрическими. Иногда еще используют комбинированную трубку Пито-Прандтля.

Высота столбика жидкости в трубке Прандтля равна пьезометрическому напору:

.

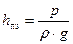Высота столбика жидкости в трубке Пито равна сумме статического и скоростного напоров:

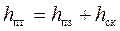
Отсюда, разность уровней столбиков жидкости в трубках Пито и Прандтля равна скоростному напору:

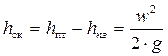
Если нижние концы трубок Пито и Прандтля находятся строго на оси трубы, то:

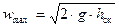, таким образом, локальную скорость на оси трубы можно определить по показателям трубок Пито и Прандтля.

Имеется важное для практики следствие из уравнения Бернулли: при сужении потока часть удельной потенциальной энергии давления переходит в удельную кинематическую энергию потока жидкости, т.е. давление понижается, а скорость увеличивается; при расширении потока – все наоборот: скорость понижается, давление увеличивается.

Примеры практического применения уравнения Бернулли – насосы, компрессоры, дроссельные расходомеры, подъемная сила крыла самолета/птицы, эффект Магнуса и т.д.