Приведение моментов и сил сопротивления, инерционных масс и моментов инерции
Система электропривода обеспечивает движение исполнительного органа через различные механические передачи. При этом движение может быть как вращательным, так и прямолинейным. Динамику электропривода оценивают принимая во внимание две или три наибольшие массы, приведенные к частоте вращения вала двигателя. В большинстве случаев упругостями элементов и воздушным зазором пренебрегают. При этом расчетную схему механизма можно представить в виде одного жесткого элемента с моментом инерции J, на который действует электромагнитный вращающий момент M и момент сопротивления Mc.
Приведение моментов сопротивления от одной оси вращения к другой может быть произведено на основании энергетического баланса системы.
 ,
,
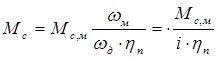 ,
,
где Мсм – момент сопротивления механизма, Мс – тот же момент, приведенный к частоте вращения вала двигателя, i – передаточное число, ηп – КПД передаточного устройства.
Приведение сил сопротивления осуществляется аналогично. Уравнение энергетического баланса
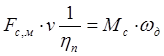 ,
,
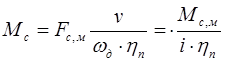
где Fc – сила сопротивления производственного механизма, v – скорость поступательного движения.
Момент инерции, приведенный к валу двигателя, определяется как
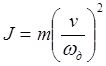 ,
,
где m – масса движущихся частей привода.
Уравнение движения
Уравнение движения используется при расчете механических переходных процессов и обычно записывается в форме Коши
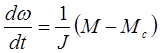 .
.
Моменты сопротивления делят на:
– реактивные – моменты от сжатия, резания и т.д., препятствующие движению исполнительного органа (меняют знак при изменении направления движения);
– активные (потенциальные) – моменты от сил тяжести, растяжения и сжатия. Названы потенциальными, поскольку связаны с изменением потенциальной энергии электропривода. Не меняют знак при изменении вращения.
Вращающий момент считается положительным, если его направление совпадает с направлением движения привода, в противном случае, он считается отрицательным.
Исходя из возможных режимов работы электропривода, уравнение движения в общем виде выглядит следующим образом
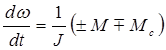 .
.
Дата добавления: 2017-06-13; просмотров: 2735;











